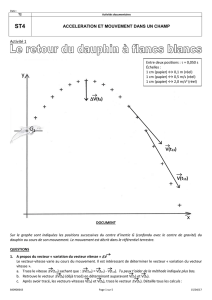
Exercice 5 : cinématique du point - Académie de Créteil

Académie de Créteil http://www.ac-creteil.fr/physique
Cinématique du point.
Version adaptée
Dans le repère (O,
kji 
 ,,
), la position d'un point M est définie à chaque instant t par
kjiOM 
 zyx 
, avec x = 2 t2 + 1 ; y = 3 t - 2 ; z = 0.
1) Quelle est l'équation cartésienne de la trajectoire ? La représenter.
2) Quelles sont les caractéristiques du vecteur vitesse ?
Calculer sa valeur
1
à l'instant t.
Le représenter aux instants t = 0 et t = 1 s.
3) Mêmes questions que 2) pour le vecteur accélération.
Réponses
1) z = 0 donc la trajectoire est dans le plan xOy
x = 2/9 ( y + 2 )2 + 1 : c'est l'équation d'une parabole de
sommet ( 1, - 2 ), de concavité tournée vers les x
positifs.
2)
dt
OMd
v
. Il a donc comme coordonnées :
dx/dt = 4 t ; dy/dt = 3 ; dz/dt = 0
A t = 0, le mobile est au point ( 1 ; - 2 ; 0 ) ; le
vecteur-vitesse est défini par dx/dt = dz/dt = 0 et
dy/dt = 3 ; il est parallèle à l'axe Oy.
A l'instant t = 1s, il est au point ( 3 ; 1 ; 0 ) ; le
vecteur-vitesse est défini par dx/dt = 4 ; dy/dt = 3 ;
dz/dt = 0.
2
9 16vt
soit v = 3 m.s-1 à l'instant t = 0 ; et
v = 5 m.s-1 à l'instant t = 1 s.
D'où les représentations des vecteurs vitesses qui
sont tangents à la trajectoire.
3)
dt
vd
a
. Il a donc comme coordonnées :
d2x / dt2 = 4 ; d2y / dt2 = d2z / dt2 = 0
Le vecteur accélération est donc constant et parallèle à Ox. Sa valeur vaut 4 m.s-2.
Version initiale
2) Quelles sont les caractéristiques du vecteur vitesse ?
Calculer sa norme à l'instant t.
Le représenter aux instants t = 0 et t = 1 s.
1
Vocabulaire : le terme norme est réservé à des grandeurs sans unités ; pour les grandeurs physiques, on utilise
le terme valeur
-6
-5
-4
-3
-2
-1
0
1
2
3
0 1 2 3 4 5 6 7 8 9 10 11 12