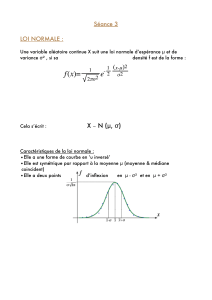
Variables aléatoires à densité

f:R→Rf
Gf
Gf
GZ+∞
−∞
f(t)tZ+∞
−∞
f(t)t= 1
x1< x2<··· < xnf x0=−∞ xn+1 = +∞
Z+∞
−∞
f(t)t
Zxi+1
xi
f(t)t0≤i≤n
Z+∞
−∞
f(t)t=
n
X
i=0 Zxi+1
xi
f(t)t
©fRf(t) = 1
2e−|t|
f
X(Ω,A,P)F
X f
∀x∈R, F (x) = Zx
−∞
f(t)t
f X
x1< x2<··· < xnf x0=−∞ xn+1 = +∞
x∈Rk∈J0, nKxk≤x<xk+1
F(x) =
k−1
X
i=0 Zxi+1
xi
f(t)t+Zx
xk
f(t)t
f f X
g f g
X

f X f
X f F
GF
Glim
x→−∞ F(x) = 0 lim x→+∞F(x)=1
GFR
GF C1
F0=f
X F
GFR
GF C1
X f =F0F
GF
GFR
GF C1
GF f =F0
0
X f
G∀a∈R,P([X=a]) = 0
G∀a, b ∈R2,P([a≤X≤b]) = Zb
a
f(t)t
X f φ X(Ω) ⊂Def(φ)
Y=φ(X)Y
X f (a, b)∈R2a6= 0
Y=aX +b
P(Y≤y)a

a= 0 Y
φ C1P(Y≤y) = P(φ(X)≤y)
φ
φ φ φ
©X f Y = exp(X)
X f n
Xn
f g R
f g
f  g :z7→ Z+∞
−∞
f(x)g(z−x)x
z∈R
X Y fXfY
Z=X+Y
fX fY
Z
fZ:t7→ Z+∞
x=−∞
fX(x)fY(t−x)x
P(Z≤z) = F(z) = Zz
t=−∞ Z+∞ x=−∞
fX(x)fY(t−x)x t
X Y X +Y
f:R→R
z7→ 
Zz
0
fX(x)fY(z−x)x z >0
0

(Xk)16k6nn fkXkFk
Mn= max
16k6nXnmn= min 16k6nXk
Gx∈RF(x) = P(Mn6x)
P(Mn6x) = P(X16x, X26x, . . . , Xn6x)
=P(X16x)P(X26x). . . P(Xn6x)
=F1(x)F2(x). . . Fn(x)
GFRC1
F1, . . . , Fn
GMnF
Gx∈RF(x) = P(mn6x)
P(mn> x) = P(X1> x, X2> x, . . . , Xn> x)
=P(X1> x)P(X2> x). . . P(Xn> x)
= (1 −F1(x))(1 −F2(x)) . . . (1 −Fn(x))
GF(x)=1−(1 −F1(x))(1 −F2(x)) . . . (1 −Fn(x))
GFRC1
F1, . . . , Fn
GmnF
X f
Z+∞
−∞
tf(t)t X
XE(X)Z+∞
−∞
tf(t)t
XRα β
αX +β
E(αX +β) = αE(X) + β

X Y
X+Y
X+Y
E(X+Y) = E(X) + E(Y)
X
X−E(X)
X f φ I
Y=φ(X)
YZ+∞
−∞
φ(t)f(t)t
E(Y) = Z+∞
−∞
φ(t)f(t)t
©
X f Y = exp(X)
X f f(t) = 1
2exp(−|t|)E(Y)
X
X
V(X) = E(X−E(X))2
X2X
X
V(X) = E(X2)−(E(X))2