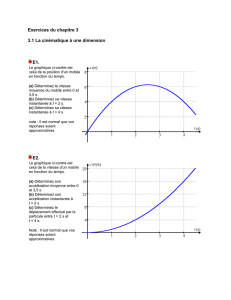
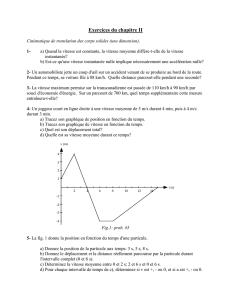
Préparation à l`évaluation

Préparation à l’évaluation
Semaine du 7 décembre
Technico-sciences 5e secondaire
1. Mireille est actuaire ; c'est-à-dire une professionnelle du monde des affaires qui
appliquent les mathématiques dans le secteur financier. Une des tâches de
Mireille est le calcul des barèmes des primes d’assurance. Pour ce faire, elle doit
entre autres faire appel à ses connaissances en algèbre et en statistique. Par
exemple, pour assurer les biens (meubles, électroménagers, appareils
électroniques, etc.) d’un appartement, la compagnie pour laquelle Marie travaille
exige 50$ de frais de base en plus de 15$ par tranche complète ou partielle de
1000$.
a) Soit x représentant la valeur monétaire des biens à assurer et f(x) le coût
de la prime, quelle est la règle représentant cette situation ?
b) À partir de la règle, déterminez quel sera le coût de la prime si la valeur
des biens à assurer est de 25 875$.
c) Un des clients de cette compagnie paie une prime de 860$ pour assurer
ses meubles, quelles sont les valeurs possibles du total de ses biens
assurables.
2. Clément, un biologiste de la vie marine, s’intéresse à différents écosystèmes.
Plusieurs données sont alors prises en considération dont la pression agissant sur
ces derniers. À la surface, la pression est de 1 bar et elle augmente de 1 kg / cm2,
c'est-à-dire 1 bar, à tous les 10 mètres de profondeur. Afin de simplifier ses
calculs, Clément considère que l’augmentation de la pression ne se fait pas
graduellement, mais qu’elle augmente par saut de 1 bar à tous les 10 mètres de
profondeur.
a) Soit x représentant la profondeur de l’écosystème et E(x) la pression en
bars, déterminez la règle qu’il utilisera afin de déterminer la pression
exercé sur l’écosystème.
b) Lors de cette étude, Clément a découvert une bactérie dite barophile, c'est-
à-dire une bactérie que l’on retrouve surtout dans les écosystèmes où la
pression est supérieure à 400 bars. Déterminez la profondeur minimale des
écosystèmes dans lesquels se développe cette bactérie.

3. Un informaticien travaille à la conception d’un nouveau logiciel qui sera utilisé en
comptabilité. Il doit intégrer une nouvelle fonction permettant d’arrondir les
nombres.
a) Puisque les comptables travaillent avec des valeurs monétaires, déterminez
la fonction qui permet d’arrondir les nombres positifs au centième inférieur
ou égal.
b) Déterminez la fonction qui permet d’arrondir les nombres négatifs au
centième supérieur ou égal.
4. L’énergie cinétique d’un objet en en mouvement est donné par l’équation
suivante :
2
2
cmv
E
où m est la masse de l’objet (en kg)
v est la vitesse de l’objet (en m/s)
et
c
E
est l’énergie cinétique (en joules).
a) Déterminez l’équation de la vitesse de l’objet en fonction de l’énergie
cinétique de ce dernier.
b) Représentez graphiquement cette fonction sachant que le masse du mobile est
de 5 kg.
c) Sachant que la vitesse du mobile est de 10 m/s, déterminez l’énergie cinétique
de ce dernier.
5. Un climatologue tente d’établir que la vitesse d’un tsunami (en m/s) est reliée à la
profondeur de l’océan (en m). Voici les données qu’il a recueillies :
Profondeur de l’océan (en m)
0
500
2000
4500
8000
Vitesse du tsunami (en km/h)
0
70
140
210
280
a) Quelle est la règle de cette fonction ?
b) Représentez graphiquement cette fonction.
c) Quelle est la vitesse du tsunami si la profondeur de l’océan est :
1) 3000 mètres 2) 5500 mètres 3) 7000 mètres

6. En économie, on utilise souvent des fonctions pour représenter la demande et
l’offre d’un produit en fonction de son prix. La demande d’un produit augmente
lorsque son prix diminue. L’offre, quant à elle, augmente lorsque le prix du
produit augmente. Le prix d’équilibre d’un produit correspond au point
d’intersection de l’offre et de la demande.
La demande d’un produit selon son prix est donnée par la fonction D(x) = 240 –
8 et l’offre par la fonction O(x) = 0,4x, où x représente le prix du produit.
En tentant de trouver le prix d’équilibre de ce produit, Maude a obtenu un résultat
d’environ 2238 $. En observant son graphique, elle se rend compte que ce résultat
est impossible. Aidez-la à déterminer le prix d’équilibre et expliquez d’où provient
son erreur.
7. Lorsqu’un corps tombe en chute libre, et que sa vitesse initiale est nulle, on peut
déterminer la hauteur de l’objet à l’aide de l’équation suivante.
h = h0 + at2, où h est la hauteur de l’objet ;
h0 est la hauteur initiale de l’objet ;
a = –9,8 m/s2 est l’accélération
gravitationnelle ;
t est le temps en secondes.
Un objet est lâché du toit d’un édifice de 80 m de hauteur. On veut connaître le
temps que met l’objet avant de toucher le sol.
a) Trouvez une fonction permettant de calculer le temps écoulé depuis que
l’objet a été lâché, en fonction de la hauteur de l’objet.
b) Représentez graphiquement cette fonction et indiquez, sur le graphique, les
points correspondant au moment où l’objet est lâché et au moment où l’objet
touche le sol.
c) Estimez le temps de chute de l’objet.
8. Anna, qui est pâtissière, confectionne au moins 60 gâteaux par semaine.
La préparation de chaque gâteau nécessite 400 g de farine, qu’Anna achète en sacs
de 2 kg. Un ami lui fait remarquer qu’en achetant des sacs de 5 kg elle
économiserait au moins 30 $ par semaine. Que pensez-vous de cette affirmation,
sachant qu’un sac de 2 kg de farine coûte 3 $ alors qu’un sac de 5 kg coûte
5,50 $ ?

9. Martin hésite entre deux forfaits proposés par deux compagnies de service
Internet, qui imposent toutes deux une limite de téléchargement de 30 gigaoctets
par mois. Le tarif de base de la première compagnie est de 32 $ par mois, auquel
s’ajoutent des frais de 6 $ pour chaque tranche complète de 1 gigaoctet
supplémentaire. Dans le cas de la seconde, les frais de base sont de 45 $ et il faut
payer 5 $ pour chaque gigaoctet complet supplémentaire. Expliquez à Martin dans
quelle circonstance le forfait de la première compagnie est le plus avantageux
et dans quelle circonstance c’est l’autre.
10. Olivier veut concevoir un jardin rectangulaire sur son terrain. La largeur du jardin
sera de 2,5 m, mais la longueur reste à déterminer. Olivier estime qu’un sac de
terre devrait être suffisant pour couvrir une surface de 3 m2 et il ne veut pas
acheter plus de 10 sacs pour son jardin. Déterminez la longueur que pourrait avoir
le jardin si Olivier se sert de 10 sacs de terre exactement.