TD 5 : Optimalité parétienne et équilibre général Exercice 5.1

TD 5 : Optimalité parétienne et équilibre général
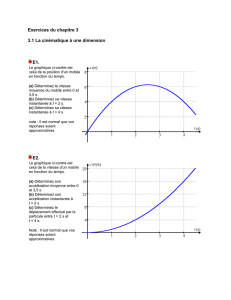
Exercice 5.1 : Optimalité parétienne
On considère une économie sans production à deux biens, notés 1 et 2, et deux agents, notés
A et B. Les biens 1 et 2 sont disponibles en quantités respectives de 4 et 4 unités. Les
préférences des agents sont représentées par les fonctions d'utilité suivantes :
2
1 2 1 2
2
1 2 1 2
( , )
( , ) 2
A a a a a
B b b b b
U x x x x
U x x x x
1. Quelles sont les conditions caractérisant un optimum de Pareto?
2. En déduire l'équation de la courbe des contrats. Représenter cette courbe dans la boîte
d'Edgeworth.
3. Que penser de l'allocation réalisable
(1,2)
a
x
et
(3,2)
b
x
?
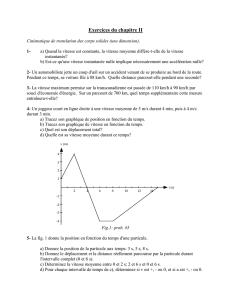
Exercice 5.2 : Equilibre général dans une économie d'échange
On considère une économie sans production à deux biens, notés 1 et 2 et deux agents, notés A
et B, dont les préférences sont représentées par les fonctions d'utilité suivantes :
1 2 1 2
1 2 1 2
( , )
( , )
A a a a a
B b b b b
U x x x x
U x x x x
Les dotations initiales des agents sont données par
12
( , ) (8,2)
a a a
et
12
( , ) (2,6)
b b b
.
1. Calculez le niveau d'utilité que chaque agent retire de sa dotation initiale. Peut-on dire que
l'agent 1 est plus satisfait par sa dotation initiale que l'agent 2 ? Que valent, pour chaque
agent, son taux marginal de substitution du bien 2 au bien 1 ?
2. Les échanges ont lieu dans le cadre walrassien et on notera
1
p
le prix du bien 1,
2
p
le prix
du bien 2. Déterminez les demandes brutes des agents, i.e. leurs niveaux de consommation
souhaités en fonction des prix. En déduire les demandes nettes individuelles
1a
z
,
2a
z
,
1b
z
et
2b
z
. Selon la valeur du prix relatif
12
/pp
, qui demande quoi et qui offre quoi ? Comparez
avec votre résultat à la question 1. Que pouvez-vous en conclure ?
3. Vérifiez que les fonctions de demande nettes respectent la loi de Walras. Représentez la
situation dans la boîte d’Edgeworth si le prix relatif vaut 1.
4. Déterminez les prix et les allocations d'équilibre général. Vérifiez qu’il s’agit bien d’un
optimum de Pareto. Représentez la situation d’équilibre dans la boîte d’Edgeworth.
Exercice 5.3 : Equilibre général avec fonctions d'utilité quasi-linéaires
Reprenez les données et la solution de l’exercice « Equilibre partiel et fonction d'utilité » du
TD 4. Rappelons que les fonctions d’utilité y étaient de type « quasi linéaires en
1
x
», i.e. du
type
1 2 1 2
( , ) ( )U x x u x ax
,
2
"( ) 0ux
.

1. Représentez la situation (allocations initiales et finales à l’équilibre, contraintes de budget
et allure générale des courbes d’indifférence) dans la boîte d’Edgeworth.
2. Calculez l’équation de la courbe des contrats et représentez-la dans la boîte d’Edgeworth.
3. Que se passerait-il si on modifiait un peu l’allocation initiale, en donnant par exemple à
Ada le panier (12,1) ou (11,0), et le reste à Bill ?
Exercice 5.4 : Equilibre général avec production
Soit une économie composée d'un ménage dont les préférences sont représentées par la
fonction d'utilité
( , )U Y Y
où Y est la quantité de bien de consommation et la quantité
de loisir. On note L la quantité de travail, sachant que le ménage dispose de 10 unités de
temps total. L’économie se compose également d'une entreprise produisant le bien en utilisant
du travail selon la technologie
YL
. On note w le salaire horaire et p le prix unitaire du
bien de consommation.
1. En sachant que le bénéfice de l'entreprise, noté π, est versé au ménage, déterminez la
demande de bien et l'offre de travail du ménage. Fournissez une représentation graphique.
2. Déterminez le bénéfice maximum de l'entreprise, son offre de bien et sa demande de
travail. Fournissez une représentation graphique.
3. Déterminez les demandes nettes de bien et de travail, notées respectivement
( , )
Y
z w p
et
( , )
L
z w p
. Vérifient-elles la loi de Walras ?
4. Ecrivez le système d'équations caractérisant l'équilibre général et déterminez les prix,
production, emploi, bénéfices à l'équilibre. Fournissez une représentation synthétique de
l’équilibre en utilisant les graphiques des questions 1 et 2.
5. Comparez le
Y
TMS 
et la productivité marginale du travail à l’équilibre. Fournissez une
représentation graphique.
6. On suppose maintenant que la fonction de production de l'entreprise est donnée par
Y aL
avec
0a
. Déterminez l'équilibre général et commentez.