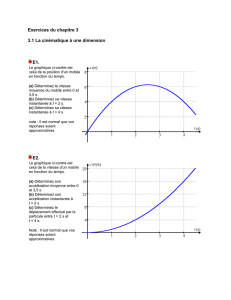
Exercice 1

1 sur 2
Chapitre 3 – Régime sinusoïdal
EXERCICES
Exercice 1
1) Déterminez UC (valeur efficace) ; conclusion ?
Exercice 2
1) Tracez l’allure générale du diagramme de Fresnel des tensions.
2) En déduire à quelle condition i/u=0.
Exercice 3
Tout dipôle peut être représenté par un modèle série d’impédance Zs=Rs+jXs ou par un modèle
parallèle d’admittance Yp=Gp+jBp (
p
pR
1
G
et
p
pB
1
X
)
1) Représentez graphiquement les deux modèles.
On appelle
p
p
s
sX
R
R
X
Q
le facteur de qualité du dipôle :
2) Déterminez l’expression de Rp en fonction de Rs et Q. Que devient cette relation si Q >> 1 ?
3) Déterminez l’expression de Xp en fonction de Xs et Q. Que devient cette relation si Q >> 1 ?
Exercice 4
1) Déterminez l’expression de ZY1, ZY2 et ZY3 en fonction de Z1, Z2 et Z3.
2) Que deviennent ces relations si Z1 = Z2 = Z3 = Z ?
Z2
i
uL
uR
uc
e(t)
R
)t314cos(210)t(e 
UR=6V
uc
u
R
L
Z3
Z1
Z2
Z3
Z1

2 sur 2
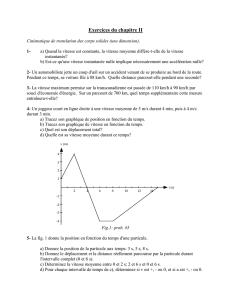
Exercice 5
u(t) est une tension alternative sinusoïdale de fréquence f réglable et de valeur efficace U=230V.
1) Déterminez l’expression du module de l’impédance équivalente au circuit R,L,C série.
2) Déterminez l’expression du déphasage i/u.
3) Tracez les courbes Z=f() et i/u=f().
4) Déterminez l’expression générale de la fréquence f0 pour laquelle Z est minimum. Que valent Z et
i/u à cette fréquence ?
5) Tracez l’allure de l’évolution de I en fonction de . Justifiez la notion de résonance pour f=f0.
6) Déterminez l’expression du rapport
U
UC
à la résonance ; conclusion ?
u(t) est maintenant un signal en créneau d’amplitude 255V et de fréquence f=50Hz
7) Déterminez l’équation de i(t) en utilisant les résultats de l’analyse de Fourier et le théorème de
superposition.
8) Tracez i(t) à l’aide de votre calculatrice graphique ; Conclusion ?
9) Quelle est la fonction réalisée par le montage ?
Exercice 6
1) Déterminez l’expression de la puissance active P fournie à la charge en fonction de E, R, X et RG.
2) A RG donné, quelle doivent être les valeurs de R et de X pour que P soit maximum ? Quelle est
alors l’expression de PMax ?
Adaptation d’impédance par réseau LC (fig.2)
3) A RG, R et X donnés, déterminez les expressions de L et de C pour que le transfert de puissance
soit maximum. Le réseau LC consomme t-il de la puissance active ?
C
jX
R
EG
RG
i
C
u
R
L
R=10
L=1H
C=10F
Générateur
Charge
jX
R
EG
RG
L
Fig.2