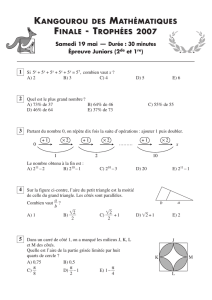
fonctions cosinus -deux

UPVM / SCIENCES / ESEU-B
Calculatrice non autorisée
Documents non autorisés
I) Equations:
1) Quel nombre x faut-il ajouter au numérateur et au dénominateur de la fraction 3/7 pour obtenir
une fraction égale au double de la première ?
2) On augmente de 3 unités la longueur x d'un carré , et l'aire augmente alors de 21 unités
d'aire. Quelle était la longueur du côté du carré ?
3) On augmente de 5 unités la longueur x d'un carré , et l'aire se trouve multipliée par 4. Quelle
était la longueur du côté du carré ?
4) On augmente de x unités la longueur d'un carré de côté 4, et l'aire augmente alors de 9 unités
d'aire. Quelle était la longueur x ajoutée ?
5) On recherche combien mesurent les côtés d’un rectangle sachant que:
- si l’on augmente la longueur de 1, l’aire augmente de 2
- si l’on augmente la largeur de 2, l’aire augmente de 6
6) On recherche combien mesurent les côtés d’un rectangle sachant que:
- si l’on augmente la longueur de 20%, le périmètre augmente de 1
- si l’on augmente la largeur de 50%, le périmètre augmente de 1.
7) On augmente de 10% la longueur et 20% la largeur d’un rectangle. Quel est le pourcentage
d'augmentation de l'aire ?
II) Géométrie et fonctions :
1) Dans le plan repèré par les axes orthonormés (Ox,Oy), on porte les points A(5,0), B(0,4),
H(3,0) et C(3,4)
a) Dessiner la figure et tracer le triangle OAC
b) Quelles sont les coordonnées du milieu I de CA ?
c) Déterminer le point D qui avec BIA constitue un parallélogramme de diagonale BA.
d) Montrer que le triangle OAC est isocèle
e) Quelle est la longueur de la hauteur issue de O ?
f) En observant les différents triangles composés avec les points OABC, déterminer la tangente
des angles (OA,OC), (CO,CH) et (CH,CA). puis celle de l’angle somme (CO,CA).
g) En utilisant le produit scalaire, déterminer le cosinus des 3 angles du triangle OAC.
h) Dans le triangle AOC, les 3 médianes se rencontrent en G et les 3 hauteurs en K. Calculer les
coordonnées de ces points G et K.
n.b.: la question h) est indépendante des questions c), e), f) et g).
2) Dans le carré OABC de côté 10 (figure) on porte:
- le point fixe I à mi-hauteur sur OB,
UPVM / SCIENCES / ESEU-B
- un point M variable sur BC, avec BM = x, et le
point N sur AC tel que CN = x (x est un paramètre).
On note f(x) l’aire du triangle IMN
a) Calculer l’aire f(x) par soustraction, en utilisant des
triangles rectangles entourant le triangle IMN.
n.b. on trouve f(x) = (x ² - 5x + 50) / 2
b) Tracer la courbe représentative de la fonction f(x)
représentant l’aire en question.
3) Dans le plan repèré par les axes orthonormés (OX,OY), avec les grandes lettres X et Y pour
désigner les coordonnées dans ces axes, on porte
- le point fixe C(3,4),
- un point M sur OX, d’abscisse 6
- le point N où la droite (CM) rencontre l’axe OY.
a) Ecrire l’équation de la droite CM (sous la forme Y = a X + b), calculer l’ordonnée Y de N et
l’aire du triangle OMN.
A partir de maintenant, on rend variable le point M sur OX, en lui donnant une abscisse égale à
un paramètre x (petite lettre)
b) Calculer, en fonction du paramètre x, l’ordonnée Y du point N construit comme avant.
c) Calculer l’aire f(x) du triangle OMN. On trouve f(x) = 4 x ²/ (x-3)
d) Etudier les variations de la fonction f , y compris les branches infinies
e) Tracer la courbe représentative de la fonction f.