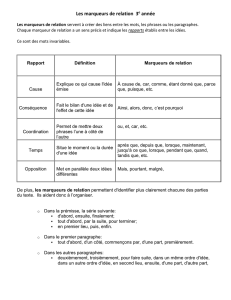
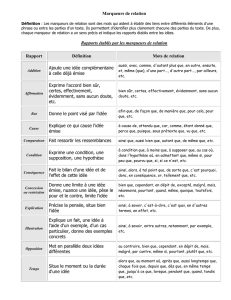
Syllabus (automne 2002)

Méthodologie du travail intellectuel
Département de philosophie de l’UQAM
Marqueurs de liens de connexion logique et de liens
d'inférence
Voici, à titre indicatif, une liste de marqueurs logiques, tirés de l’ouvrage de
Gilles Doyon et Pierre Talbot (1986) : La logique du raisonnement: La logique du
raisonnement:théorie de l'inférence propositionnelle et applications (Sainte-Foy:
Le Griffon d'Argile (collection philosophie).
Marqueurs d’affirmation
Il est vrai que p
On peut affirmer que p
On peut dire que p
Sans l’ombre d’un doute, p
En fait, p
En vérité, p
Il est certain que p
Il est sûr que p
Or, p
Soit p
Sans conteste, p
Il est évident que p
De toute évidence, p
Etc.
Marqueurs de conjonction
p et q
À la fois p et q
Non seulement p, mais aussi q
p, toutefois (pourtant, mais) q
p, bien que (quoique) q
p, de plus (également) q
p, malgré que q
p. Enfin (Ensuite) q
p. En plus q
p, encore que (alors que) q
p. Qui plus est q
p. De surcroît q
p. Or q
Etc.
Marqueurs de conséquence
1. Implication
si p alors q
lorsque p, q
q à condition (pourvu) que p
q si p
p implique (entraîne) q
p implique matériellement q
2. Équivalence
p si et seulement si q
p si q et q si p
si p alors q, et réciproquement
p est équivalent à q
p est matériellement équivalent à q
Etc.
Marqueurs de négation
Il est faux que p
On peut nier que p
On ne peut affirmer (dire) que p
Il n’est pas possible que p
p (cela) n’arrive pas
p (cela) ne se produit pas
... ne ... pas (jamais, point, plus, etc.)
... ne ...
Aucun ....
Nul ...
ni ... (ni ....)
Personne ne
On n’a pas p
Etc.

Marqueurs de disjonction
1. Disjonction non exclusive (inclusive)
p ou q, ou les deux
p ou q
p et/ou q
Etc.
2. Disjonction exclusive
p ou q
p ou q, mais pas les deux
p ou alors q
soit p, soit q
p à moins que q
p sauf si q
ou bien p ou bien q
Etc.
Marqueurs d’incompatibilité
Il est impossible que p et à la fois que q
Il est impossible que p et en même
temps que q
Il est incompatible que p et que q
Il est faux à la fois que p et que q
On ne peut pas p et à la fois q
p n’est pas compatible avec q
p ne peut pas arriver (se produire) en
même temps que q
Etc.
Marqueurs de prémisse
car
parce que
la raison en est que
puisque
en effet
Etc.
Marqueurs de conclusion
Donc p
Ainsi p
En conséquence p
C’est pourquoi p
D’où p
Par suite p
Nous en inférons que p
Nous en déduisons que p
Nous en concluons que p
Il s’ensuit que p
Il s’ensuit logiquement que p
Alors p
Tout ceci implique que p
Etc.
2