PC* Étude des coniques planes d`équation

R2R2
(O, i, j)
ax2+ 2bxy +cy2=K
Γax2+ 2bxy +cy2=K(a, b, c)̸= (0,0,0)
A=a b
b c ̸= (0)
(x, y)Ax
y= (x, y)ax +by bx +cy=ax2+ 2bxy +cy2
A D ∈ M2(R)P∈ O2(R)
D=α10
0α2=tP AP avec tP=P−1
sp(A) = {α1, α2}det(A) = α1α2=ac −b2r(A) = α1+α2=a+c
(e1, e2)M(i,j)(e1, e2) = P M
(x, y) (O, i, j) (x′, y′) (O, e1, e2)
x′
y′=P−1x y=tPx y
M∈Γ⇔K=ax2+ 2bxy +cz2= (x, y)Ax
y= (x′, y′)tP AP x′ y′
M∈Γ⇔K= (x′, y′)Dx′
y′= (x′, y′)α10 0α2x′ y′=α1x′2+α2y′2
Γ (O, e1, e2)α1x′2+α2y′2=K
det(A) = α1α2= 0 α1= 0
Γα2y′2=K
◦K= 0 Γ y′= 0
◦Kα2<0 Γ = ∅
◦Kα2>0 Γ
y′=±K/α2
•det(A) = α1α2>0
Γ
◦K= 0 Γ = O
◦K α1α2Γ = ∅

◦K, α1, α2
x′2
a2+y′2 b2= 1 a=K/α1>0, b =K/α2>0
Γ (O, e1) (O, e2)
•det(A) = α1α2<0
Γ
◦K= 0 Γ
y′=±kx′k=−α1/α2
◦K̸= 0 Γ
x′2
a2−y′2 b2=±1
Γ (O, e1) (O, e2)
0< b < a (E)
(O, e1, e2)
(E)x2
a2+y2 b2= 1
(E) (O, e1) (O, e2)
(E)x=acos(t)y=bsin(t)t∈[0,2π]
–2
–1
1
2
–2 –1 1 2
x≥0y≥0M(x, y)∈(E)⇔y=b1−x2
a2

a b
(H) (O, e1, e2)
(E)x2
a2−y2 b2= 1
(H) (O, e1) (O, e2)
H)
x=a ch(t), y =b sh(t)t∈R+
y=±b/ax (H)
–4
–2
0
2
4
–6 –4 –2 2 4 6
x
x≥0y≥0M(x, y)∈(H)⇔y=bx2
a2−1
(O, e1, e2)
(P) : x=ay2+b
–3
–2
–1
1
2
3
–8 –6 –4 –2 2 4 6 8 10
(O, e1)S(b, 0)
x=at2+b, y =t t ∈R

Γ (O, i, j)
ax2+ 2bxy +cy2+dx +ey =K(a, b, c)̸= (0,0,0)
F: (x, y)7→ ax2+ 2bxy +cy2+dx +ey
F C∞R−−→ gradF (x, y) = (2ax + 2by +d, 2bx + 2cy +e)
(x, y)Fax +by =−d/2
bx +cy =−e/2
det(A) = ac −b2
•det(A)̸= 0 X0(x0, y0)
M(x, y) (X0, i, j)x′=x−x0, y′=y−y0
F(x, y) = a(x0+x′)2+2b(x0+x′) (y0+y′)+c(y0+y′)2+d(x0+x′)+e(y0+y′)
F(x, y) = ax2
0+ 2bx0y0+cy2 0+dx0+ey0+ax′2+ 2bx′y′+cy′2
+2ax0x′+ 2bx0y′+ 2by0x′+ 2cy0y′+dx′+ey′
F(x, y) = F(x0, y0) + ax′2+ 2bx′y′+cy′2
Γ (X0, i, j)
ax′2+ 2bx′y′+cy′2=K−F(x0, y0)
det(A)̸= 0
•det(A) = 0
a̸= 0 x0=−d/2a y0= 0
ac =b2
ax′2+ 2bx′y′+cy′2=ax′+b
ay′2
+−b2
a+cy′2=ax′+b ay′2
Γ (X0, i, j)
ax′+b
ay′2
+ey′=K′
◦e̸= 0
◦e= 0
A
Γ
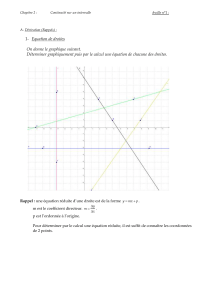
x2−xy +y2+ 2x+ 3y=K x2+xy +y2+ 2x+ 3y=K