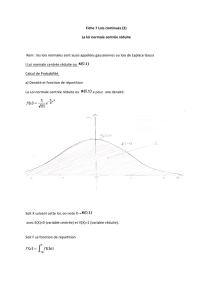
4 Loi normale centrée réduite

www.mathasingapour.canalbog.com
Loi normale centrée réduite
Définition
Comment calculer une probabilité (à la calculette) :
On ne peut calculer l’intégrale "à la main" : pas de primitive directe
Avec la Ti-nspire : menu – probabilité – distribution – Normal FdR
Comment déterminer x connaissant la probabilité P( X < x )
Avec la Ti-nspire :
menu – probabilité – distribution
– Inverse Normale
La loi normale centrée réduite, notée N (0 ; 1),
est la loi ayant pour densité de probabilité
la fonction f définie sur
!
par
f x
( )
=1
2 !
e
!x2
2
Si X est une variable aléatoire qui suit la loi
normale centrée réduite N (0 ; 1), alors :
P a !X!b
( )
!=!1
2 !
e"x2
2dx
a
b
#!

www.mathasingapour.canalbog.com
Symétrie de la courbe
Propriété : intervalle associé à une probabilité donnée
Pour déterminer
u
!
, on va d’ abord
trouver son opposé
!u
!
à la calculette sachant que :
P X ! " u
!
( )
=
!
2
Exemple : pour
! =0,10
On a :
1! ! =0, 90
On va résoudre
P X ! " u
!
( )
=0, 05
à la calculette
On obtient :
!u
!
" !1, 645
Par conséquent
P!1, 645 "X"1, 645
( )
#0, 9
P X ! " x
( )
!!=!!P X #x
( )
P!x"X"x
( )
!!=!!2#P0"X"x
( )
P X !0
( )
!!=!!P X "0
( )
!!=!1
2
P X !x
( )
!!=!! 1
2
!"!P0#X#x
( )
Soit X une variable aléatoire de loi N (0 ; 1).
Pour tout α dans
0;1
] [
, il existe un unique réel positif
u
!
tel que :
P!u
!
"X"u
!
( )
=1! !