Fiche 7 Lois continues (2) La loi normale centrée réduite Rem : les lois

Fiche&7&Lois&continues&(2)&
La&loi&normale&centrée&réduite&
!
!Rem!:!les!lois!normales!sont!aussi!appelées!gaussiennes!ou!lois!de!Laplace!Gauss!
I!Loi!normale!centrée!réduite!ou!! !
Calcul!de!Probabilité.!
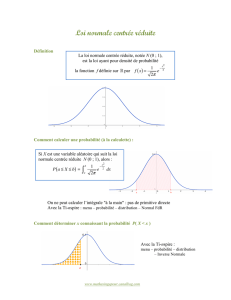
a)!Densité!et!fonction!de!répartition!
La!Loi!normale!centrée!réduite!ou!! !a!pour!!une!densité:!
! !
!
Soit!X!suivant!cette!loi,!on!note!X→!
!avec!E(X)=0!(variable!centrée)!et!V(X)=1!(variable!réduite).!
!
Soit!F!sa!fonction!de!répartition!
!

!
Cette!intégrale!ne!peut!être!exprimée!par!des!fonctions!usuelles.!Il!existe!donc!des!tables.!(p166)!
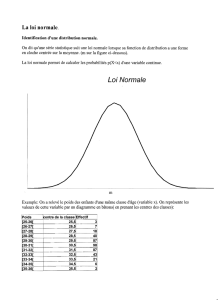
b)!Utilisation!de!la!table!de!la!fonction!de!répartition!de!la!loi!!! !!pour!le!calcul!de!probabilité.!
Soit!!X!→,!
!calculer!les!probabilités!suivantes!en!utilisant!la!propriété!F(Mx)=1MF(x)!:!
p(X<1,23)!p(0<X<1,23)!p(0,36<X<1,23)!
p(X<M0,88)!p(M0,88<X<0)!p(M0,88<X<1,23)!
p(X>M2,25)!p(X>2,25)!p(X≥1,23)!
p((X>2,23)ou(X<M1,49))! ! p(X≤0)! ! p(X=1,23)!
p(|X|<2)!
//!Film!loi!de calcul!de!proba.!
!
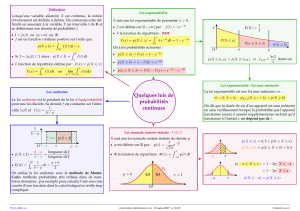
II!Quantiles!de!la!loi! !
On!note!Uα!le!quantile!α!de!la!loi!! ,!!c'estMàMdire!le!réel!qui!vérifie!F(Uα)=p(X<Uα)=α!ainsi!pour!
lecture!de!la!table!:!
U0,99=!2,33!

!
Propriété!U1Mα!=!MUα!
a)!Calculer!les!quantiles!:!
α!
0,75!
0,8413!
0,9!
0,95!
0,975!
0,9771!
0,99!
0,9987!
Uα!
!
!
!
!
!
!
!
!
Calculer!U1Mα/2!pour!!α=0,05!
!!!α=0,1!
!!!α=0,01!
α!
0,1!
0,5!
0,05!
0,01!
Uα!
!
!
!
!
!
//!Film!quantiles!! !
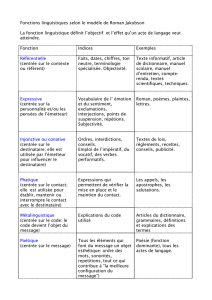
b)!Intervalles!centrés!de!probabilité!donnée!
Vérifiez!que!p(Ma<X<a)=2!F(a)M1!
Calculez!p(M1,96<X<1,96)!
Trouvez!a!tel!que!p(Ma<X<a)=0,9!puis!0,99!
!!!!!puis!0,5!
!!!!!puis!1Mα!!!!!
//!Film!intervalles!centrés!!! !