I- DÉRIVATION EN UN POINT 1) Taux de variation 2) Nombre dérivé

COURS N°5 : DÉRIVATION
Maths–1èreSTI
1
I- DÉRIVATION EN UN POINT
1) Taux de variation
Définition
: pour toute fonction numérique f définie sur un intervalle I, et a, b deux
réels distincts de I, le taux de variation de f entre a et b est le nombre réel m défini
par :
Remarque
: m est le coefficient directeur de la droite passant par les points A et B de
coordonnées respectives (a ; f(a)) et (b ; f(b)).
Exemple
:
f est la fonction définie sur [0 ; +∞[ par :
√.
Le taux de variation de f entre 1 et 0 est :
√0√1
01 1
Soient A et B les points de coordonnées
respectives (1, 1) et (0, 0). Le coefficient
directeur de (AB) est égal à 1.
2) Nombre dérivé
a)
Définition
f est une fonction définie sur un intervalle I, a et a + h sont deux réels de I.
Notons T(h) le taux de variation de f entre a et a + h :
Définition 1
: soit f une fonction définie sur un intervalle I ; a et a + h deux réels de I.
f est dérivable en a, signifie qu’il existe un nombre réel L tel que :
lim
Le nombre L est appelé nombre dérivé en a de f, on le note f’(a).

COURS N°5 : DÉRIVATION
Maths–1èreSTI
2
Remarque
: « f’(a) » se lit « f prime de a ».
Exemple
: utiliser la définition précédente pour démontrer que la fonction f définie sur
par 23 est dérivable en -1. Nous préciserons le nombre dérivé f’(1).
Comportement du taux de variation (0) :
1
1
21 3
1
2
2
lim
1 1
2
Ainsi, f est dérivable en -1 et f’(-1) = 2.
b)
Interprétation graphique - tangente
Soit C la courbe représentative, dans le plan muni d’un
repère ;, , d’une fonction f et a un réel appartenant à
son ensemble de définition Df.
Soit un réel h 0 tel que a + h appartienne à Df.
• Le taux de variation
de f entre a et a
+ h est le coefficient directeur de la droite (AM),
avec ; et ;
.
• Si f est dérivable en a, ce coefficient
admet pour limite f’(a) lorsque h
tend vers 0.
Graphiquement, le point M se rapproche de A en restant
sur la courbe C, et la droite (AM) tend à occuper une
position limite .
La droite est la tangente à C au point A.
Définition 2
: soit f une fonction numérique définie sur un intervalle I. Soit a un réel
de I tel que f soit dérivable en a, de nombre dérivé L = f’(a). On note C la courbe
représentative de f dans un repère orthogonal du plan. La tangente à C au point
A(a ; f(a)) est la droite passant par A de coefficient directeur L.
Animation « skieur »
: http://missiontice.ac-besancon.fr/lp_maths_sciences/tableau_virtuel/maths/geogebra/derivee/pe_nombre_derivee.htm

COURS N°5 : DÉRIVATION
Maths–1èreSTI
3
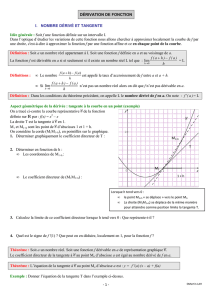
Exemple 1
: sur le graphique ci-dessous, on a tracé la courbe C représentant la
fonction f ainsi que ses tangentes aux points A, B et C. Déterminer graphiquement les
nombres dérivés de f en 0, 1 et 3.
• La tangente en A(0 ; 3) a pour coefficient directeur 0,
donc f’(0) = 0.
• La tangente en B(1 ; 0,5) a pour coefficient directeur
-5, donc : f’(1) = -5.
• La tangente en C(3 ; 0,5) a pour coefficient directeur
1, donc f’(3) = 1.
Exemple 2
: activité Euler n° 52
(passage de 4 élèves au tableau).
Théorème
: soit f une fonction numérique dérivable en un réel a de nombre dérivé
L = f’(a). Soit C sa courbe représentative dans le plan muni d’un repère orthogonal.
L’équation réduite de la tangente à C au point d’abscisse a est :
.
Démonstration
: d’après la définition précédente, la tangente à C au point a, a pour
coefficient directeur f’(a), donc a une équation de la forme :
avec .
De plus, comme ∆,
; ce qui donne
.
On remplace alors dans la première expression :
Exemple
: f est la fonction définie sur par :
. Soit C sa courbe
représentative dans le plan muni d’un repère orthogonal ;, .
On cherche l’équation réduite de la tangente à C au point A d’abscisse 3.
3
3
² 6 9 9
6
6
lim
3 3
6
Ainsi, f est dérivable en -3 et f’(-3) = -6.
On en déduit que l’équation réduite de la tangente à C au point A est :
6
3
969

COURS N°5 : DÉRIVATION
Maths–1èreSTI
4
II- DÉRIVATION SUR UN INTERVALLE – FONCTION DÉRIVÉE
1) Définition
On établit dans cette partie des méthodes de calcul qui permettront de ne pas avoir à
utiliser la définition 1 précédente pour chaque calcul d’un nombre dérivé d’une fonction
f
en
a
.
On va voir comment, si une fonction est dérivable pour toutes les valeurs d’un intervalle, on
peut établir une formule de calcul pour tous les nombres dérivés de cette fonction sur cet
intervalle.
Exemple
: soit la fonction f définie sur par f(x) = x² et dérivable sur . Etudions la
dérivabilité de f en
a
, sans donner de valeur numérique à
a
.
²
2
lim
2
On en déduit que la fonction f est dérivable pour tout réel
a
et que le nombre dérivé de
f en
a
est f’(
a
) = 2
a
.
On peut donc facilement déterminer le nombre dérivé d’un réel quelconque, sans avoir a
effectuer le développement de f(
a
+
h
) : f’(2) = 4 ; f’(-3) = -6 ; f’( 5) = 2 5…
Définition
: soit f une fonction définie un intervalle I. f est dite dérivable si et
seulement si, pour tout a I, f admet un nombre dérivé en a. La fonction définie sur I
qui, à tout réel a de I, associe le nombre dérivé de f en a est appelée fonction dérivée
de f. Cette fonction est notée f’.
Exemple
: la fonction f : x
x² est dérivable sur et f’ : x 2x.
2) Fonctions dérivées des fonctions usuelles
A partir de la définition et par le même type de calcul que celui fait dans l’exemple du
paragraphe précédent, on démontre les résultats suivants que l’on admettra ici.

COURS N°5 : DÉRIVATION
Maths–1èreSTI
5
Fonction f définie sur : Par : Dérivable sur : Fonction dérivée f’
définie par :
(n entier
strictement positif)
∞,0
0, ∞
∞,0
0, ∞
²
∞,0
0, ∞
nentier
strictementpositi
f
∞,0
0, ∞
0, ∞
√ 0, ∞
√
3) Opérations sur les fonctions dérivables
a)
Résultats
Soit u et v deux fonctions définies et dérivables sur un même intervalle I. On admettra les
résultats suivants :
Opération Fonction définie
sur : Par : Dérivable sur : Fonction dérivée
définie par :
Addition I I
Multiplication
par un réel I avec
I
Multiplication I I
Carré I² I
Division I 0
I 0
²
Inverse I 0
I 0
²
Fonction
composée
I é
I é
 6
6
 7
7
 8
8
1
/
8
100%