la fonction exponentielle

Terminales ES Ch10. La fonction exponentielle Année 2010–2011
1
LA FONCTION EXPONENTIELLE
I.Introduction :
On sait que la fonction logarithme f(x) = ln x est une fonction définie et strictement croissante sur ] 0 ; + [.
L'équation ln x = b, avec b réel quelconque, admet donc une unique solution dans ] 0 ; + [ .
Cette solution est nommée exponentielle de b et notée exp(b) .
On définit ainsi une nouvelle fonction , notée exp , à valeurs dans ] 0 ; + [.
1) Définition :
La fonction exponentielle , notée exp , est une fonction définie sur IR , à valeurs dans ] 0 ; + [.
On a : si x > 0 et b IR ln x = b x = exp(b)
On a donc :
En remplaçant x par exp(b) dans ln x = b on obtient ln ( exp(b) ) = b.
On dit que les fonctions ln et exp sont des fonctions réciproques l'une de l'autre.
ln : ] 0 ; + [ IR exp : IR ] 0 ; + [
x ln x x exp(x)
2) Exemples de valeurs :
ln 1 = 0 1 = exp(0) ; ln e = 1 e = exp(1) ; ln e3 = 3 ln e = 3 e3 = exp(3)
Si p IN ln ep = p ln e = p ep = exp(p)
Cette dernière propriété à donné l'idée de noter cette nouvelle fonction exponentielle de la manière
suivante : exp(x) = ex pour tout x de IR .
On pourra utiliser indifféremment les deux notations .
exp(0) = e0 = 1 ; exp(1) = e1 = e ; exp(3) = e3 ; ln x = b x = eb ; ln ( ex ) = x .
II. Formules:
1) Exponentielle d'un logarithme :
ln ( ex ) = x avec x IR .
Si x > 0 ln x = b x = eb = exp( ln x ) en remplaçant b par ln x .
si x > 0 eln x = exp( ln x ) = x
2) Exponentielle d'une somme :
ln ( ea eb ) = ln ( ea ) + ln ( eb ) = a + b = ln ( ea + b )
donc ln (ea eb ) = ln ( ea + b ) ea eb = ea + b
Exemple : e3 e5 = e8
3)Exponentielle élevée à une puissance :
ea eb = ea + b si on remplace b par a dans la formule on obtient ea ea = ( ea )² = e2a
e2a ea = ( ea )² ea = ( ea )3 = e3a.
On peut généraliser cette formule . Si n ZZ , ( ea )n = ena.
Application : (e4 )3 = e12

Terminales ES Ch10. La fonction exponentielle Année 2010–2011
2
4) Exponentielle d'une différence :
ln ea
eb = ln ( ea ) – ln ( eb ) = a – b = ea – b donc ea
eb = ea – b = ea eb
Application : si a = 0 alors on a 1
eb = e–b
III. Etude de la fonction exponentielle:
Ensemble de définition : IR
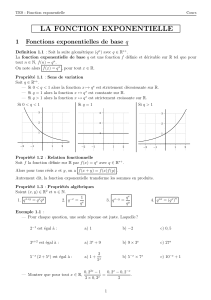
Tracé de la courbe représentative de la fonction exponentielle :
x
– 2
– 1
0
0,5
1
1,5
2
2,5
3
exp(x)
0,14
0,37
1
1,65
2,72
4,48
7,39
12,18
20,09
Dérivée :
Posons g(x) = ln ( ex ) . On a donc g(x) = x donc g'(x) = 1
Si on dérive directement g(x) à l'aide des fonctions composées, on a g'(x) = (ex )'
ex .
Donc (ex )'
ex = 1 ( ex )' = ex
La fonction exponentielle est dérivable sur IR et (ex )' = ex . Elle est sa propre dérivée.
De plus , comme la fonction exp est à valeurs dans ] 0 ,+ [ on a (ex )' > 0 pour tout x de IR .
La fonction exponentielle est donc strictement croissante sur IR .
Tableau de variations :
x
–
+
(ex)'
+
ex
0
+
exp
ln
y = x
Les courbes des fonctions logarithme
et exponentielle sont symétriques par
rapport à la droite d'équation y = x .

Terminales ES Ch10. La fonction exponentielle Année 2010–2011
3
Limites et asymptotes :
lim
x – ex = 0 donc la droite d'équation x = 0 est asymptote à la courbe représentative de la fonction exp .
lim
x + ex = + et lim x + ex
x = + .
Primitive de ex :
Les primitives de la fonction f (x) = ex sont F(x) = ex + k , k IR .
Résolutions d'équations et d'inéquations :
La fonction ex est strictement croissante sur IR donc
ea = eb a = b et ea > eb a > b.
Exemple : Résoudre e 5x – 2 = e –3x + 1 et e x² – 1 e x + 1
e 5x – 2 = e –3x + 1 5x – 2 = – 3x + 1 8x = 3 x = 3
8 S = { 3 8 }
e x² – 1 e x + 1 x² – 1 x + 1 x² – x – 2 0 = 9 x1 = – 1 et x2 = 2
donc S = ] – ; – 1 ] [ 2 ; + [
IV. Etude des fonctions eu , avec u une fonction dérivable sur un intervalle I de IR :
1) Dérivée de eu
Si f(x) = eu(x) alors f '(x) = u'(x) eu(x) . ( fonctions composées )
Exemple : Calculer la dérivée de f(x) = e 3x² – 2x + 9
On pose u(x) = 3x² – 2x + 9 u'(x) = 6x – 2 donc f '(x) = ( 6x – 2 ) e 3x² – 2x + 9
2) Primitive de u' eu , avec u une fonction dérivable sur un intervalle I de IR :
Si f(x) = u'(x) eu(x) alors f admet des primitives de la forme F(x) = eu(x) + k , k IR .
Exemple : Calculer la primitive de f(x) = – 2 e 3x – 5
u(x) = 3x – 5 u'(x) = 3 donc f(x) = – 2
3 3 e 3x – 5 = – 2 3 u'(x) eu(x)
donc F(x) = – 2
3 e3x – 5 + k k IR .