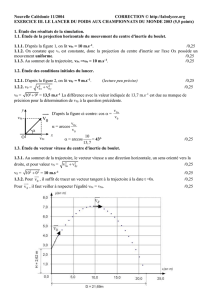
On lâche un objet ponctuel sans vitesse initiale à l`altitude y=h à t=0

NumerikSciences © copyright
1
On lâche un objet ponctuel sans vitesse initiale à l’altitude y=h à t=0
Expression des composantes vx0(t) et vy0(t) du vecteur vitesse 
v0x= 0 et v0y=0
Système : objet de centre G
Bilan des forces : poids P
Seconde loi de Newton :
gmP
dt
vd
mamFext
donc
ga 
Coordonnées de l’accélération et de la vitesse
a
aX=0 primitive
v
vX(t) = v0x = 0 v0x et v0y sont les conditions
initiales
aY= g vY(t) =
y
vtg 0
=
tg
Coordonnées x et y:
v
vX(t) = v0x =0 primitive
OG
x(t)=
0
0x
(à t=0 x0 = 0 et y0=h )
vY(t) =
tg 
y(t)=
h
tg
y
tg 
22
2
0
2
Le mouvement sera rectiligne uniformément accéléré .
y
x
O
h

NumerikSciences © copyright
2
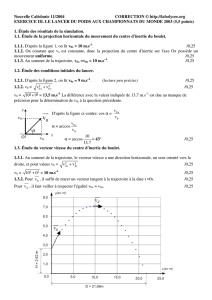
On lance un objet considéré comme ponctuel de masse m dans un champ de
pesanteur uniforme.
On place un repère de façon à étudier le mouvement de cet objet.
Expression des composantes vx0(t) et vy0(t) du vecteur
vitesse 
v0x= v0×cosα et v0y=v0×sinα
Système : objet de centre G
Bilan des forces : poids P
Seconde loi de Newton :
gmP
dt
vd
mamFext
donc
ga 
Coordonnées de l’accélération et de la vitesse
a
aX=0 primitive
v
vX(t) = v0x =
cos
0v
v0x et v0y sont les conditions initiales
aY= -g vY(t) =
sin
00  vtgvtg y
Coordonnées x et y:
v
vX(t) = v0x =
cos
0v
primitive
OG
x(t)=
00 cos xtv 
(à t=0 x0 = 0 et y0=0 )
vY(t) =
sin
00  vtgvtg y
y(t)=
00
2sin
2ytv
tg 
x(t)
cos
0
v
y(t)
tv
tg 
sin
20
2
Equation de la trajectoire :
Dans x(t), on isole t : t =
cos
0vx
on remplace t dans y(t) :
y(x)=
cos
sin
2
cos
0
0
22
0
2
v
x
v
v
x
g
en simplifiant on trouve :
xx
v
g
xy
A
)(tan.
cos2
)( 2
22

NumerikSciences © copyright
3
L’équation est de type y = ax2 + bx + c c’est l’équation d’une parabole.
Entrainement avec des situations différentes :
Si l’objet se trouve à t=0 à une altitude y0=h alors
l’équation de la trajectoire sera :
Si l’objet est lancé avec une vitesse horizontale
V0x = v0 et V0y=0
Alors