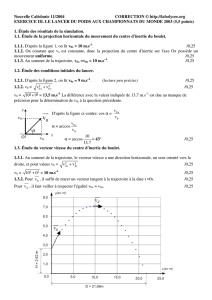
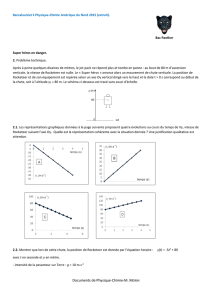
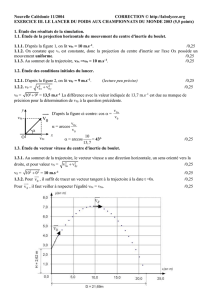
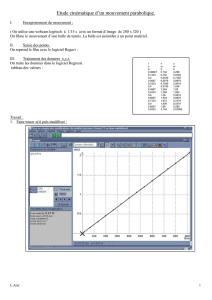
29. On désigne la vitesse fournie v = 7,6i+6 ,1j (considérée en unités

29. On désigne la vitesse fournie v =7,6
i+6,1 j(considérée en unités SI) par v1, par opposition à la vitesse de la balle
lorsqu’elle atteint sa hauteur maximale, symbolisée par v2, et la vitesse à laquelle elle retourne au sol, représentée
par v3. On pose que v0est la vitesse de lancement, comme d’habitude. L’origine se situe au niveau du sol, au point
où la balle est lancée.
a) À l’aide de l’équation 3.16, on détermine que
v2
1y=v2 0y
−2g∆y
6,12=v2
0y
−2(9,8)(9,1),
ce qui donne v0y14,7 m/s. Sachant que v2ydoit être égal à 0, on utilise encore l’équation 3.16 mais, cette fois,
avec ∆y=hcomme hauteur maximale:
v2
2y=v2 0y
−2gh
0=14,72 −2(9,8)h,
ce qui équivaut à h11 m.
b) En se rappelant la démarche pour l’obtention de l’équation 4.30, mais en remplaçant v0sin
θ
0par v0yet
v0cos θ
0par v0x,on obtient
0=v0yt−
1
2gt2
R=v0xt,
ce qui mène à R=2v0xv0y
g. Sachant que v0xv1x7,6 m/s, on obtient R2(7,6) (14,7)/9,8 23 m.
c) Comme v3xv1x7,6 m/s et que v3yv0y14,7 m/s, on a
v3=v2
3x+v2 3y=(−14,7)2+7,62=17m/s.
d) L’angle (mesuré par rapport à l’horizontale) de v3est une des possibilités suivantes:
tan−1−14,7
7,6=−63◦ou 117◦.
On choisit la première possibilité (soit 63°) puisque les signes des composantes indiquent que le vecteur se
trouve dans le quatrième quadrant. Le vecteur vitesse v3effectue un angle de 63° sous l’horizontale.