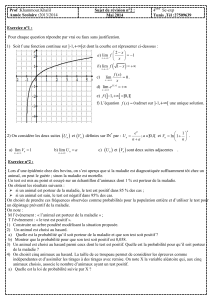
L`année 2011-2012 complète

MATHÉMATIQUES
TERMINALE ES
A. YALLOUZ
Ce polycopié conforme au programme 2002, regroupe les documents distribués aux élèves en cours d’année.
Année 2011-2012

Lycée Camille SEE
Année 2011-2012 Tle ES
A. YALLOUZ (MATH@ES) 2

TABLE DES MATIÈRES
IENSEIGNEMENT OBLIGATOIRE 5
1DÉRIVATION 6
I Nombre dérivé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
II Fonction dérivée . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2CONTINUITÉ ET RÉSOLUTION D’ÉQUATIONS 22
I Fonction continue . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
II Résolutions d’équations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3LIMITES 31
I Notion de limite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
II Limites de fonctions usuelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
III Règles opératoires sur les limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
IV Limite par comparaison . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
4STATISTIQUES À DEUX VARIABLES 45
Activité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
I Ajustement affine d’une série statistique à deux variables . . . . . . . . . . . . . . . . . . . . . . 49
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
5PRIMITIVES D’UNE FONCTION 58
Activités . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
I Primitives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
II Calculs de primitives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
6LOGARITHME NÉPÉRIEN 66
Activité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
I Fonction logarithme népérien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
II Propriétés algébriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
III Étude de la fonction logarithme népérien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
IV Étude d’une fonction ln(u). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
7PROBABILITÉS 88
I Modéliser une expérience aléatoire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
II Probabilités conditionnelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
III Variable aléatoire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
IV Loi binomiale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
A. YALLOUZ (MATH@ES) 3

Lycée Camille SEE
Année 2011-2012 TABLE DES MATIÈRES Tle ES
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
8CALCUL INTÉGRAL 114
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
I Intégrale d’une fonction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
II Propriétés de l’intégrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
III Intégrale et moyenne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
9FONCTION EXPONENTIELLE 129
I Définition et premières propriétés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
II Propriétés algébriques de la fonction exponentielle . . . . . . . . . . . . . . . . . . . . . . . . . . 130
III Étude de la fonction exponentielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
IV Exponentielle d’une fonction : exp(u). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134
V Exponentielle de base a. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138
II ENSEIGNEMENT DE SPÉCIALITÉ 155
10 INTRODUCTION À LA THÉORIE DES GRAPHES 156
Activités : Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157
I Graphes premières définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157
Activité : Chaîne eulérienne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162
II Chaînes, cycles ; connexité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163
III Coloration des sommets d’un graphe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
IV Plus court chemin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172
11 GÉOMÉTRIE DANS L’ESPACE 184
I Vecteur de l’espace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 185
II Repérage dans l’espace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 185
III Équations cartésiennes de l’espace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 186
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189
12 FONCTION DE DEUX VARIABLES 195
I Fonction de deux variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 196
II Sections de surface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 196
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 200
13 RAISONNEMENT PAR RÉCURRENCE 214
I La démonstration par récurrence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 215
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216
14 SUITES 217
I Suites premières définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 218
II Comportement global d’une suite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219
III Limite d’une suite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221
IV Suites particulières . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 222
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228
15 GRAPHES PROBABILISTES 236
I Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 237
II Évolution d’un état au cours du temps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 238
EXERCICES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 241
A. YALLOUZ (MATH@ES) 4

PREMIÈRE PARTIE
ENSEIGNEMENT OBLIGATOIRE
A. YALLOUZ (MATH@ES) 5