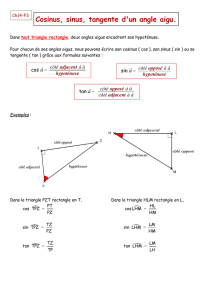
Le Savant Cosinus

Le Savant Cosinus
François Rideau
Sachant qu’en 12 minutes il monte 0 voyageur,
dans combien de temps appellera-t-on le n0720 ?
Christophe. L’idée fixe du Savant Cosinus
1. Introduction
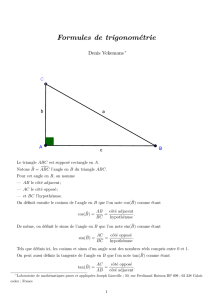
La plupart des points remarquables d’un triangle ABC ont des coordonnées
barycentriques qui s’expriment simplement au moyen des lignes trigonométriques
des angles , , du triangle. Citons quelques exemples :
• Le centre de gravité G : (1,1,1).
• Le centre du cercle circonscrit O : .
• Le centre du cercle inscrit I : .
• L’orthocentre H : .
• Le point de Gergonne Γ: .
On va poser les questions suivantes :
Problème. Soit ABC un triangle d’un plan affine euclidien.
1. Reconnaître le point Ωde coordonnées barycentriques
,
c’est-à-dire en donner une construction simple.
2. Montrer que les points G, Ω, Γsont alignés.
2. Existence du point Ω
Tout d’abord le point Ωexiste car la somme des masses
En effet on a :
(1)
et
(2)
cos cos cos cosCAB AB A
µ µ µ µ µ
µ
()
=−−
()
=− +
()
=− + π12
2
BB
2
µ
cos cos cos cosA B AB
2
AB
2
µ µ
µ µ µ µ
()
+
()
=+
−
2 
cos cos cos .ABC
µ µ µ
()
+
()
+
()
≠0
cos , cos , cosA BC
µ µ µ
()
()
()
()
tan , tan , tan
A
2
B
2
C
2
µ µ µ
tan , tan , tanABC
µ µ µ
() () ()
()
sin , sin , sinABC
µ µ µ
()
()
()
()
sin , sin , sin222ABC
µ µ µ
()
()
()
()
C
µ
B
µ
A
µ
249
Pour chercher et approfondir
APMEP
no457
Rideau-Texte 22/03/05 9:08 Page 249

APMEP
no457
Donc
Comme on a les inégalités
il en résulte que :
et, par suite,
Pour éviter des maux de tête à ceux que rebute trop de trigonométrie, on peut
aussi appliquer les relations métriques entre angles et côtés d’un triangle :
(3)
Donc
à cause des inégalités triangulaires.
3. Construction du point Ω
L’idée est évidemment de construire les points d’intersection respectifs L, M, N
des droites AΩ, BΩ, CΩavec les côtés BC, CA, AB du triangle.
Là aussi, c’est un peu l’inconvénient de la géométrie affine, il faut montrer
l’existence de ces points. En vertu de l’associativité barycentrique, L est le
barycentre des points massiques et , M celui des points
massiques et et N celui des points massiques
et .
Il faut donc montrer les inégalités
BB;cos
µ
()
()
AA;cos
µ
()
()
AA;cos
µ
()
()
CC;cos
µ
()
()
CC;cos
µ
()
()
BB;cos
µ
()
()
cos cos cosABC
µ µ µ
()
+
()
+
()
=+−++−bca
bc
cab
22 2 2 2
2
22222
222
22ca
abc
ab
ab c a bc a b ca
++−
=+− + +− + +()( )(
bbc
abc
−> )
20
abc bc
bca ca
ca
222
222
22
2
2
=+−
()
=+−
()
=
cos
cos
A
B
µ
µ
++−
()
bab
2
2cosC
µ
cos cos cos .ABC
µ µ µ
()
+
()
+
()
>1
sin , sin , sin
ABC
µ µ µ
20202
>
>
>00,
022 022 022 <<<<<<
ABC
µ µ µ
πππ
,,,
cos cos cos cos cA BC AB
2
µ µ µ
µ µ
()
+
()
+
()
=+ + 12 ooscos
si
AB
2
AB
2
µ µ µ µ
−
−+
=+14nnsinsin.
A
2
B
2
C
2
µ µ µ
250 Pour chercher et approfondir
Rideau-Texte 22/03/05 9:08 Page 250

Si on avait , on aurait en vertu de l’égalité (1) :
Mais
entraînerait =0, ce qui est absurde car >0.
De même
entraînerait :
ce qui est aussi absurde car
Les deux autres inégalités se démontrent de façon analogue par permutations
circulaires.
On peut encore éviter cette débauche de trigonométrie de la façon suivante :
à cause des inégalités triangulaires.
Pour construire le point L barycentre des points massiques et
, on va regarder trois cas de figure :
1. Les angles , sont aigus. Alors et (voir figure 1).
Le point L est situé sur le segment BC.
cos C
µ
()
>0
cos B
µ
()
>0
C
µ
B
µ
CC;cos
µ
()
()
BB;cos
µ
()
()
cos cosAB
µ µ
()
+
()
=+−++−
=
bca
bc
cab
ca
ab
222222
2
22
++−
()
++−
()
=++
()
−+
ca bcab
abc
ababc ab
22 222
2
2
() ())
() ()
()
aabb
abc
abc ab
abc
ab
22
22
2
2
−+
()
=+−−
()
=+(()()cabcab
abc
+− −+ >
20
00<< <<A B
µ µ
ππ,.
AB
µ µ
−=π,
cos AB
2
µ µ
−
=0
C
µ
C
µ
cos sin
AB
2
C
2
µ µ µ
+
= =0
cos cos .
AB
2
AB
2
µ µ µ µ
+
− =0
cos cosAB
µ µ
()
+
()
=0
cos cos , cos cos , cosB CCAA
µ µµ µµ
()
+
()
≠
()
+
()
≠
()
00++
()
≠cos .B
µ
0
251
Le savant Cosinus
APMEP
no457
Rideau-Texte 22/03/05 9:08 Page 251

APMEP
no457
La perpendiculaire en B au côté AB et la perpendiculaire en C au côté AC se
coupent au point A′diamétralement opposé au point A sur le cercle circonscrit
au triangle ABC. Compte tenu des hypothèses faites sur les angles et ,
les points A et A′sont de part et d’autre de la droite BC. Soit U le point où la
bissectrice intérieure de l’angle coupe la médiatrice de BC et V le point où
la bissectrice extérieure de l’angle coupe cette même médiatrice. Les points
U et V sont diamétralement opposés sur le cercle circonscrit au triangle ABC.
Comme et , on a :
Il en résulte que la droite A′L est la bissectrice intérieure au sommet A′du
triangle A′BC. Cette bissectrice est aussi la droite A′V , laquelle est parallèle à
la droite AU. Autrement dit, dans ce cas de figure, la droite A′Lest parallèle à
la bissectrice intérieure de l’angle du triangle ABC.
2. L’un des angles ou est supérieur à et supposons que ce soit pour
fixer les idées (voir figure 2). Les points A et A′sont cette fois dans le même
demi-plan délimité par la droite BC.
B
µ
π
2
C
µ
B
µ
A
µ
sin sin cos ,
sin
′
()
=−
=
()
′
(
ABC B B
ACB
· µµ
·
π
2
))
=−
=
()
sin cos .
π
2CC
µµ
′=−ACB C
· µ
π
2
′=−ABC B
· µ
π
2
A
µ
A
µ
C
µ
B
µ
252 Pour chercher et approfondir
A
BC
O
U
V
L
A
FIG. 1 – Le premier cas.
′A
Rideau-Texte 22/03/05 9:08 Page 252

Comme et , le point L est sur la droite BC à l’extérieur
du segment BC. Comme et , on a :
Il en résulte que la droite A′L est la bissectrice extérieure au sommet A′du
triangle A′BC. Cette bissectrice est aussi la droite A′V , laquelle est parallèle à
la droite AU. Autrement dit, dans ce cas de figure aussi, la droite A′L est encore
parallèle à la bissectrice intérieure de l’angle du triangle ABC.
3. L’un des angles ou est droit et supposons que ce soit l’angle . Les
points A′et L sont confondus avec C et L appartient encore à la droite CV
symétrique de la bissectrice intérieure AU par rapport au centre O.
La construction du point Ωest donc claire : on trace les droites symétriques des
bissectrices intérieures aux sommets A, B, C du triangle ABC par rapport au centre
O du cercle circonscrit au triangle ABC. Ces droites concourent évidemment au point
J symétrique de I par rapport à O. La droite A′J coupe le côté BC au point L de
coordonnées barycentriques , la droite B′J coupe le côté CA au
0,cos ,cosBC
µ µ
()
()
()
B
µ
C
µ
B
µ
A
µ
sin sin cos ,
sin
′
()
=−
=−
()
′
ABC B B
ACB
· µµ
·
π
2
(()
=+
=
()
sin cos .C C
µµ
π
2
′=+ACB C
· µ
π
2
′=−ABC B
· µ
π
2
cos C
µ
()
>0
cos B
µ
()
<0
253
Le savant Cosinus
APMEP
no457
A
BC
O
U
V
L
A
FIG. 2 – Le deuxième cas.
′A
Rideau-Texte 22/03/05 9:08 Page 253