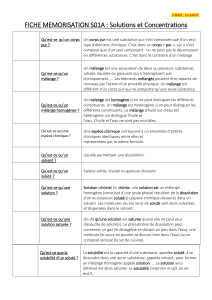
molécules chimique solvant plusieurs

2016-11-052016-11-05 1
Thermodynamique
statistique biomoléculaire
GBM2620
Automne 2016
Chapitre 16 de
Molecular Driving Forces
Michael D. Buschmann et Marc Lavertu

2016-11-052016-11-05 2
Chapitre 16 : Solvatation et transfert
de molécules entre phases
Dans ce chapitre, on s’intéresse à la solvatation et à la
partition de particules d’une espèce chimique dans un
milieu composé d’une autre espèce chimique.
Par exemple, certaines toxines se dissolvent dans un milieu tel que
l’eau et s’accumulent dans un autre, tel que le gras de poisson.
On va aussi déterminer comment des molécules modifient
l’équilibre de phase pour des molécules d’une autre espèce
chimique.
L’ajout de sel fait fondre la glace et fait augmenter le point d’ébullition
de l’eau.
Différences de potentiel chimique est la force motrice :
1) Les particules ont tendance à se déplacer vers des régions où leur
concentration est plus faible afin d’augmenter l’entropie (s).
2) Les particules ont tendance à se déplacer vers des régions pour
lesquelles elles ont une plus grande affinité chimique (enthalpie h).
Michael D. Buschmann et Marc Lavertu

2016-11-052016-11-05 3
La solvatation est le transfert de
molécules entre un gaz et un liquide
On considère un mélange liquide de deux composants A et B,
B (l’eau) est volatil, A (sel) ne l’est pas:
B peut se déplacer librement entre la phase gazeuse et le liquide.
Le degré de liberté du système est le nombre de molécules de type B
dans le gaz ou le nombre de molécules dans le liquide .
Pour un sel (A) dissout dans l’eau (B), l’eau est plus volatil.
On peut aussi avoir un gaz (B volatil) dissout dan l’eau (A moins volatil)
La condition d’équilibre à constantes est
D’après les chapitres 11 (Eq. 11.50) et 15 (Eq.15.17)
Michael D. Buschmann et Marc Lavertu
( ) ( )
BB
gl
µµ =
et Tp
( ) ( )
( )
( )
2
0,int
ln ln 2 1
µµ
χ
=
= ++ −
BB
B B B BB AB B
gl
kT p p kT x zw kT x
( )
B
Ng
( )
B
Nl

2016-11-052016-11-05 4
Modèle du réseau pour solvatation et
diminution de la pression de vapeur
On peut exprimer dans une forme plus compacte:
où (Eq. 14.9) est la tension de vapeur de B
au-dessus d’une solution pure de B ( )
Dans le cas d’une solution idéale ( ),
est une fonction linéaire de , c’est la
loi de Raoult.
B a plus tendance à s’échapper lorsque
et moins lorsque .
Lorsque , la solution se comporte comme
si elle était idéale, peu importe la valeur de .
Michael D. Buschmann et Marc Lavertu
B
p
( )
()
( )
()
22
ln 21 21
0,int
B BB AB B BB AB B
x zw kT x zw kT x
BB
B
pe xe
p
χχ + +− +−
⇒= =
B
p
()
()
2
1
0AB B
x
B BB
p pxe
χ −
=
( )
2
00
,int
BB
zw kT
BB
p pe=
0
AB
χ >
0
AB
χ =
B
x
(~idéal)
0
AB
χ <
1
B
x→
AB
χ
1
B
x→
1=
B
x

2016-11-052016-11-05 5
Modèle du réseau pour solvatation et
diminution de la pression de vapeur
L’ajout d’une faible quantité de sel à de l’eau pure diminue sa
pression de vapeur. Pourquoi si l’énergie d’interaction ne joue
aucun rôle ( ) ?
L’ajout de A (sel) diminue la tendance à s’échapper de B (eau). Comme
pour l’idéalité dans un gaz parfait, l’idéalité en solution ( )
décrit des processus dont la force motrice est l’entropie de translation
et non pas l’énergie d’interaction.
Pour un liquide pur de B,
Quand des molécules A sont ajoutées,
Michael D. Buschmann et Marc Lavertu
0
1 ln 0, 1 2
B BB B
W S k W x zw µµ =⇒= = =⇒= =
0 ou 1
AB B
x χ = →
1W=
1W>
( )
( )
2
0
00
1 0, ln 1
ln si 0 ou 1
B B B AB B
BB BBB AB B
W S kT x kT x
kT x x
µµ χ
µµ µχµ
>⇒ > = + +
= →⇒ <
−
= +
** car les B ont principalement B
comme voisin proche, comme dans une phase pure de B.
ne dépend pas de lorsque 1
B AB B
x µχ →
0 ou 1
AB B
x
χ = →