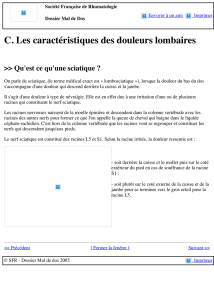
Racines de l`unité

Atelier de découverte
Atelier de découverte du Deug MIAS 1999-2000
par E.Cousquer (USTL)
Etude des racines de l’unité, des sous-groupes et des polynômes
associés à ces racines.
Préliminaires :
– On désigne par Ul’ensemble des nombres complexes eiθ de
module 1. Il forme un groupe pour la multiplication, (le justi-
fier). Pour chaque élément eiθ de U, donner le polynôme irré-
ductible de R[x]dont il est racine.
– On désigne par Un, l’ensemble des racines n ièmes de l’unité,
pour nentier. Montrer que Unest un sous-groupe fini de U.
– Pour chaque racine n -èmes rde l’unité, on montrera que l’en-
semble des puissances distinctes de r,Gr={r, r2, r3, ...}forment
un sous-groupe de Un.
Des exemples pour se faire une idée :
– Placer sur le cercle les racines 6 ièmes de l’unité. Si r1=e2iπ
6,
on désignera par rk=e2ikπ
6, la racine rk
1et on appelle racine
primitive sixième de l’unité, une racine sixième de l’unité qui
n’est pas racine pième pour p < 6. Quelles sont les racines pri-
mitives sixièmes de l’unité? Quel est le nombre de ces racines
primitives?
Pour chaque racine r, donner le sous-groupe Grassocié à cette
racine. Quel est le sous-groupe associé à une racine primitive?
Décomposer le polynôme x6−1en facteurs irréductibles dans
R[x]. Donner le polynôme dont les racines sont exactement les
racines primitives sixièmes de l’unité.
– Faites le même travail avec les racines douzièmes de l’unité.
1

Conjectures et démonstrations Si r=e2iπ
n, et si rk=rk, quel est le
nombre d’éléments de Gr? À quelle condition sur k,rkest-elle une
racine primitive n ièmes de l’unité? Quel est le sous-groupe associé
à une racine primitive?
Application : Quelles sont les racines primitives 24 ièmes de l’unité?
Décomposer le polynôme x24 −1en facteurs irréductibles dans R[x].
Comment peut-on à partir des coefficients de ces polynômes irréduc-
tibles trouver les valeurs de cos(kπ
12 )pour les différentes valeurs de
k?Quel est le polynôme dont les racines sont exactement toutes les
racines primitives 24-ièmes de l’unité?
2

Préliminaires
– L’ensemble Udes nombres complexes eiθ de module 1 est
stable par multiplication, par passage à l’inverse et contient
l’unité de la multiplication. Il forme donc un sous-groupe de
C∗.
Nous distinguerons la racine 1de l’unité et son polynôme asso-
cié x−1, la racine −1et son polynôme associé x+1. Les autres
racines de l’unité sont de la forme eiθ. Pour chaque élément
eiθ, le polynôme irréductible de R[x]dont il est racine est le
polynôme du second degré dont les racines sont eiθ et e−iθ soit
P(x) = (x−eiθ)(x−e−iθ)ou encore P(x) = x2−2 cos θx+1.
– Comme le produit dans Cest commutatif, si zet z0sont des
racines nimes de l’unité, on a :
zn= 1,z0n= 1,(zz0)n=znz0n= 1.
Unest donc stable par multiplication et contient l’unité. D’autre
part si zn= 1 on a (z−1)n= 1. Donc Unest donc stable par
passage à l’inverse d’un élément. Les racines nimes de l’unité
sont les nombres complexes de la forme z=e2ikπ
n; elles sont
donc en nombre fini.
Unest donc un sous-groupe fini de U.
– Soit rune racine nime de l’unité. Alors pour toute valeur de
l’entier k rkest aussi une racine nime de l’unité. En effet :
(rk)n=rnk = (rn)k= 1 Donc l’ensemble Grest contenu
dans Un
Grest stable par multiplication : rk×rk0=rk+k0, il contient
l’unité puisque rn= 1, et chaque élément rka son inverse rn−k
dans Gr.
Grest donc un sous-groupe de Un.
Des exemples pour se faire une idée
Racines sixièmes de l’unité
r1=e2iπ
6=eiπ 3
3

r2=e4iπ
6=e2iπ 3
r3=e6iπ
6=eiπ =−1
r4=e8iπ
6=e4iπ 3
r5=e10iπ
6=e5iπ 3
r6=e12iπ
6=e2iπ = 1
Racines primitives sixièmes de l’unité : On peut remarquer que r2et r4
sont des racines troisièmes de l’unité, que r3est une racine carrée
de l’unité et que r6est l’unité. Les racines primitives sixièmes de
l’unité sont donc les deux racines r1et r5.
Sous-groupes associés Nous calculons les puissances successives de
chaque racine :
Gr1={r1, r2, r3, r4, r5,1}
Gr2={r2, r4,1}
Gr3={r3,1}
Gr4={r4, r2,1}
Gr5={r5, r4, r3, r2, r1,1}
Gr6={1}
On constate que le sous-groupe engendré par une racine primitive
sixième de l’unité est le groupe U6.
Décomposition du polynôme x6−1dans R[x].On utilise des identités
remarquables connues :
x6−1 = (x3−1)(x3+1) = (x−1)(x2+x+1)(x+1)(x2−x+1)
et l’on voit que les racines primitives sixièmes de l’unité sont exacte-
ment les racines du polynôme Φ6(x) = x2−x+1 (appelé polynôme
cyclotomique).
4

Racines douzièmes de l’unité
r1=e2iπ
12 =eiπ 6racine 12 ième de 1.
r2=e4iπ
12 =e2iπ 6racine 6 ième de 1.
r3=e6iπ
12 =eiπ 2=iracine 4 ième de 1.
r4=e8iπ
12 =e2iπ 3racine 3 ième de 1.
r5=e10iπ
12 =e5iπ 6racine 12 ième de 1.
r6=e12iπ
12 =eiπ =−1racine carrée de 1.
r7=e14iπ
12 =e7iπ 6racine 12 ième de 1.
r8=e16iπ
12 =e4iπ 3racine 3 ième de 1.
r9=e18iπ
12 =e3iπ 2=−iracine 4 ième de 1.
r10 =e20iπ
12 =e5iπ 3racine 6 ième de 1.
r11 =e22iπ
12 =e11iπ 6racine 12 ième de 1.
r12 =e24iπ
12 =e2iπ = 1
Racines primitives douzièmes de l’unité : On peut remarquer que :
r2et r10 sont des racines sixièmes de l’unité,
r3et r9sont des racines quatrièmes de l’unité,
r4et r8sont des racines troisièmes de l’unité,
r6est une racine carrée de l’unité,
r12 est l’unité,
r1,r5,r7et r11 sont les quatre racines primitives douzièmes de
l’unité.
Sous-groupes associés On calcule les puissances successives de la
racine.
Gr1={r1, r2, r3, r4, r5, r6, r7, r8, r9, r10, r11,1}
Gr2={r2, r4, r6, r8, r10,1}
Gr3={r3, r6, r9,1}
Gr4={r4, r8,1}
Gr5={r5, r10, r3, r8, r1, r6, r11, r4, r9, r2, r7,1}
Gr6={r6,1}
5