chapitre 1 : puissances, calcul litteral

Master 1, UE 4 , EC4A : Eléments de géométrie chapitre 3 éléments de géométrie plane Page 1
3. CORRIGES DES PROBLEMES : PARALLELISME, PERPENDICULAIRES,
FIGURES PLANES ELEMENTAIRES.
Problème 1 :
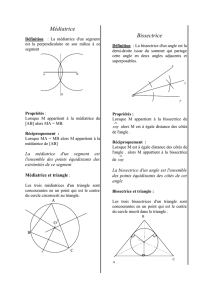
O est sur la médiatrice de [AB] donc OA = OB et O est sur la médiatrice de [AC] donc OA = OC donc
O est équidistant des points A, B et C. Donc le cercle de centre O et de rayon OA passe par les points
B et C. Comme O est équidistant de B et C, il appartient à la médiatrice de [BC], donc les médiatrices
des trois côtés du triangle sont concourantes en un point noté ici O.
Problème 2 : concours
a/ un angle de 90° : on trace une droite puis une perpendiculaire à cette droite avec le compas.
b/ un angle de 45° : on trace alors la bissectrice au compas de cet angle droit.
c/ un angle de 60° : on trace un triangle équilatéral
d/ un angle de 30° : on trace la bissectrice d’un des angles de 60°.
Problème 3 : concours
a/ Deux figures possibles : le trapèze rectangle et un quadrilatère avec deux angles opposés à 90°.
b/ impossible, s’il a 3 angles droits, il en a quatre et donc il est un rectangle !
c/ d/ possible, il suffit que les diagonales en se coupent pas en leur milieu.
Problème 4 :
Tracer un segment [AC] de 10 cm puis la perpendiculaire à (AC) passant par A.
Placer le point B sur cette perpendiculaire tel que AB = AC en reportant la longueur avec le compas.
Tracer la médiatrice de [AC], puis le demi-cercle de diamètre [AC] dont le centre est le point
d’intersection de cette médiatrice avec [AC]. Ce demi-cercle passe par A et est extérieur au triangle
ABC. Cet arc de cercle coupe la médiatrice de [AC] en D.
Problème 5 : concours Chaque réponse sera justifiée.
a/ il s’agit de l’ensemble des points du demi-plan contenant A et limité par la médiatrice de [AB].
b/ donc AM < BM (1) et AM < AB (2).
La condition (1) rappelle le a/, pour la condition (2), l’ensemble des points M est le disque de centre A
et de rayon AB (privé du cercle).
L’ensemble cherché est l’intersection du demi-plan et du disque privé du cercle.
c/ Si ABM est un triangle rectangle en A, l’ensemble des points M est la perpendiculaire à la droite
(AB) passant par A privé de A.
Si ABM est un triangle rectangle en B, l’ensemble des points M est la perpendiculaire à la droite (AB)
passant par B privé de B.
Si ABM est un triangle rectangle en M, l’ensemble des points M est le cercle de diamètre AB privé de
A et B.
L’ensemble cherché est la réunion de ces trois ensembles.