Fonction continue sur un intervalle

Fonction continue sur un intervalle – Continuité – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
1
Sont abordés dans cette fiche : (cliquez sur l’exercice pour un accès direct)
 Exercice 1 : montrer qu’une fonction est continue en un point
 Exercice 2 : dire si une fonction est continue sur un intervalle d’après sa représentation graphique
 Exercice 3 : préciser sur quel intervalle une fonction est continue (continuité des fonctions usuelles)
 Exercice 4 : étudier la continuité d’une fonction construite par opérations (somme, produit, différence)
 Exercice 5 : définir une fonction continue sur un intervalle en fonction d’un paramètre
 Exercice 6 : étudier le prolongement par continuité d’une fonction
 Exercice 7 : étudier la continuité d’une fonction composée
 Exercice 8 : utiliser le théorème des valeurs intermédiaires (fonction continue sur un intervalle)
 Exercice 9 : utiliser le corollaire du théorème des valeurs intermédiaires (fonction continue strictement
monotone sur un intervalle)
 Exercice 10 : étudier la continuité d’une fonction en utilisant le théorème des gendarmes
 Exercice 11 : écrire un algorithme d’encadrement par dichotomie
Accès direct au site www.sos-devoirs-corriges.com
Fonction continue sur un intervalle – Continuité
Exercices corrigés

Fonction continue sur un intervalle – Continuité – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
2
Soit la fonction  définie sur 
 par 
. Montrer que  est continue en 2.
Rappel : Continuité d’une fonction en un point
Soit  une fonction définie sur  et soit .
 est continue en  si et seulement si  a une limite en  égale à , c’est-à-dire si et seulement si
. En particulier  est continue en  si et seulement si 
.
Remarque : On note indifféremment la limite à gauche de la fonction  en  
 ou 
 et la
limite à droite de la fonction  en  
 ou 
.
Etudions la continuité de la fonction  en 2.
D’une part, 
.
D’autre part, on a 
.
Ainsi, 
 donc la fonction  est continue en 2.
Rappel important : Une fonction ne peut pas être continue en un point (ou un intervalle) où elle n’est pas
définie. Autrement dit, l’étude de la continuité d’une fonction en un point qui n’appartient à l’ensemble de
définition de la fonction n’a aucun sens.
Exercice 1 (1 question) Niveau : facile
Correction de l’exercice 1  Retour au menu

Fonction continue sur un intervalle – Continuité – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
3
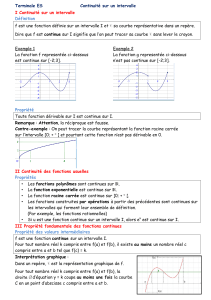
Dans un repère orthonormé  du plan, ,  et  sont les représentations graphiques respectives des
fonctions ,  et , définies sur .
Pour chacune de ces trois fonctions, dire si la fonction est continue sur .
Rappel : Représentation graphique d’une fonction et continuité
Graphiquement, on peut reconnaître qu’une fonction est continue sur un intervalle  lorsqu’on peut tracer sa
courbe représentative de manière continue, c’est-à-dire sans lever le crayon. Par ailleurs, une fonction n’est pas
continue en un point   lorsqu’on doit lever le crayon en .
La fonction  est continue sur . De même, la fonction  est continue sur .
La fonction  est continue sur  et sur  mais n’est pas continue en 3 puisque 
 et
.
Exercice 2 (1 question) Niveau : facile
Correction de l’exercice 2  Retour au menu

Fonction continue sur un intervalle – Continuité – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
4
Pour chacune des fonctions suivantes, rappeler sur quel(s) ensemble(s) la fonction est définie et continue.
1) 
La fonction  est une fonction polynôme (à coefficients réels), définie et continue sur .
2) 
La fonction  est la fonction valeur absolue, définie et continue sur .
3) 
La fonction  est la fonction racine carrée, définie et continue sur .
4) 
La fonction  est la fonction inverse, définie et continue sur  et sur .
5) 
La fonction  est la fonction cosinus, définie et continue sur .
6) 
La fonction  est la fonction sinus, définie et continue sur .
7) 
Rappel : Partie entière d’un réel et fonction partie entière
La partie entière d’un nombre réel  est l’unique entier qui lui est immédiatement inférieur ou égal. On la
note . Pour tout , on a donc .
La fonction partie entière est la fonction définie sur  qui, à tout réel , associe sa partie entière . La
fonction partie entière  est donc ainsi définie : 
Exercice 3 (1 question) Niveau : facile
Correction de l’exercice 3  Retour au menu

Fonction continue sur un intervalle – Continuité – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
5
La fonction  est la fonction partie entière, définie sur . Cette fonction est continue en toute valeur réelle
non entière mais n’est pas continue en toute valeur réelle entière. Autrement dit, la fonction  est continue sur
.
En effet, pour tout , d’une part 
 et d’autre part  .
8) 
La fonction  est la fonction exponentielle, définie et continue sur .
9) 
La fonction  est la fonction logarithme népérien, définie et continue sur 
.