TD 7 Alcènes-Correction

TD n°7 – Chimie Organique – Analyse élémentaire et Alcènes (première partie) – Correction partielle
1
TD n°7
Chimie Organique
Analyse élémentaire et Alcènes (première partie)
Correction Partielle
Exercice 1 (Analyse élémentaire)
On procède à la combustion de 36 mg d’un liquide organique ne contenant que du carbone, de l’oxygène et de l’hydrogène.
Pour ce faire, on introduit ce liquide dans une enceinte contenant du dioxygène en excès. Après passage de l’étincelle
électrique, le volume du système passe de 100 à 83,2
cm
3
.
On soumet ce dernier au contact d’une solution d’hydroxyde de potassium, le volume de gaz est encore réduit : il passe à
38,4
cm
3
.
Les volumes de gaz ont tous été mesurés dans les conditions normales où le volume molaire est de 22,4
L
mol
.
−1
.
D’autre part, la densité de vapeur étudiée par rapport à l’air est 2,5.
1) A partir de la valeur de la densité du gaz, trouver la masse molaire du produit inconnu et en déduire une relation
entre le nombre d’atomes de carbone, d’hydrogène et d’oxygène contenus dans la molécule.
2) Ecrire la réaction qui se produit lors du déclenchement de l’étincelle, en indiquant la phase des espèces
intervenantes. Mettre en équation la première variation du volume de gaz.
3) Ecrire les réactions qui se produisent avec la potasse, en indiquant la phase des espèces intervenantes. Mettre en
équation la variation du volume de gaz.
4) Déterminer la formule brute de cette substance. Déterminer le nombre et la nature possible des insaturations de
cette substance. A quelles molécules cette formule brute peut-elle correspondre ?
Le composé étudié, noté A, ne comportant que des atomes de carbone, d’oxygène et
d’hydrogène : on peut rechercher sa formule brute sous la forme CxHyOz. On a trois
inconnues : x, y et z. Il nous faut donc trouver trois équations.
1) Détermination de la masse molaire de A. 1
ère
équation liant x, y et z.
Donnée : la densité de vapeur de A, par rapport à l’air, vaut 2,5.
Par définition, la densité d’un gaz est le rapport de la masse volumique de ce gaz sur la masse
volumique de l’air, dans les mêmes conditions de température et de pression.
(
)
( )
dgaz
air
=µ
µ
Pour un mélange parfait de gaz parfaits, à température et à pression fixées, le volume molaire
Vm est indépendant de la constitution dudit mélange. On en déduit la relation suivante qui lie
densité et masses molaires :
. . .
air air m
A A A A A
A air A air air m air air
V V V
m n M M M
d
V m V n M V M M
= = = =
On peut considérer pour calculer la masse molaire de l’air que celui-ci est constitué de 80%
de diazote et de 20% de dioxygène. On a donc :
( )
(
)
(
)
1
22
.8,28
5
.4
−
=
+
≈molg
OMNM
airM
On en déduit la masse molaire de A :
(
)
1
.0,72
−
=molgAM
On en déduit la première équation liant x, y t z :
(
)
(
)
(
)
(
)
OzMHyMCMxAM ++= .
2) Réaction de combustion. 2
ème
équation liant x, y et z.

TD n°7 – Chimie Organique – Analyse élémentaire et Alcènes (première partie) – Correction partielle
2
Données : On effectue la réaction de combustion de 36 mg de A en présence d’un excès de
dioxygène (ce qui ne peut être vérifié qu’a posteriori). Le volume initial de 100 cm
3
est
ramené à 83,2 cm
3
.
On sait que toute combustion d’une substance organique consomme du dioxygène pour
engendrer l’apparition de dioxyde de carbone et d’eau.
Dans les conditions normales de pression et de température, on peut proposer l’équation -
bilan suivante :
( ) 2( ) 2( ) 2 ( )
4 2 2
x y z l g g l
y z y
C H O x O xCO H O
+ + − → +
En supposant à nouveau que le gaz est un mélange parfait de gaz parfaits, on peut écrire :
1 1
.
gaz
m
V n V
∆ = ∆
On appelle nA la quantité de matière initiale du composé A :
4
5,0.10
A
AA
m
n mol
M
−
= =
D’après l’équation-bilan,
4
2
01
yz
nn
gaz
−
=∆
On obtient une deuxième équation liant y et z :
1
2
.
4
A m
z y
V n V
−
∆ =
3) Dissolution du dioxyde de carbone en milieu basique. 3
ème
équation liant x, y
et z.
Donnée : on soumet le gaz à une solution basique d’hydroxyde de potassium. Le volume est
réduit de 83,2 cm3 à 38,4 cm3.
La solubilité du dioxyde de carbone augmente lorsqu’on se place en milieu basique, grâce à la
formation d’ions carbonate et d’ions hydrogénocarbonate.
)(
2
)(
2aqg
COCO =
)(
3
)(
2aq
aq
HCOHOCO
−−
=+
2
3 ( ) 3 ( ) 2aq aq
HCO HO CO H O
− − −
+ = +
La diminution de volume correspond donc à la dissolution du dioxyde de carbone.
2 2
.
gaz
m
V n V
∆ = ∆
2
gaz
A
n n x
∆ =
Ce qui nous donne une troisième équation :
2 0
. .
m
V n xV
∆ =
4) Détermination de la formule brute de A.
On dispose d’un système de 3 équations – 3 inconnues qui ne pose pas de difficulté pour sa
résolution ; on obtient pour formule brute de A : C
4
H
8
O.

TD n°7 – Chimie Organique – Analyse élémentaire et Alcènes (première partie) – Correction partielle 3
5) Nombre d’instaurations :
C e composé comporte une insaturation (
2 4 8 2
1
2
i
× − +
= =
) : un cycle ou une double liaison (C=C ou C=O) .
Isomères possibles :
OH
OH
OH
OH
OH
OH
OH
OH
OH
OH
OH OH
O
O
O
OH
O
O
O
O
OH
OH
O
OHOH
OHOH
HO
O
O
O
OOO
O
O
O
O
O
Exercice 3
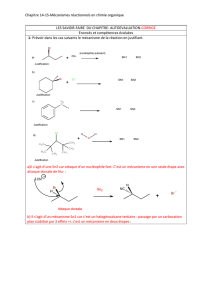
Dans les réactions suivantes, il n’y a pas d’addition sur le noyau benzénique.
1) Justifier la réaction suivante :
Cl
HCl
(rendement 80 %)
2) Quel est le produit (très majoritaire) formé par addition de l’iodure d’hydrogène sur le 1-phénylprop-1-ène ?
3) Proposer une explication de l’obtention majoritaire du 1-méthoxy-2-méthylpropan-1-ol par action de l’eau, en
milieu acide, sur le 1-méthoxy-2-méthylprop-1-ène.
H Cl
Pas de mésomèrie sur ce carbocation.
Il est donc moins stable que le précédent.
Et le produit chloré issu de ce carbocation est donc
minoritaire (la réaction étant sous contrôle cinétique,
c'est le postulat de Hammond qui nous permet
d'arriver à cette conclusion).
1)
H Cl
2)
Pas de mésomèrie sur ce carbocation.
Il est donc moins stable que le précédent.
Et le produit chloré issu de ce carbocation est donc
minoritaire (la réaction étant sous contrôle cinétique,
c'est le postulat de Hammond qui nous permet
d'arriver à cette conclusion).

TD n°7 – Chimie Organique – Analyse élémentaire et Alcènes (première partie) – Correction partielle 4
H Cl
3
)
Pas de mésomèrie sur ce carbocation.
Il est donc moins stable que le précédent.
Et l'alcool issu de ce carbocation est donc
minoritaire (la réaction étant sous contrôle cinétique,
c'est le postulat de Hammond qui nous permet
d'arriver à cette conclusion).
O
O
O
O
Exercice 4
Proposer un mécanisme rendant compte des observations expérimentales suivantes :
1)
H
2)
H
H
1)
Ce carbocation est le plus stable car il est stabilisé par
mésomérie. D'après le postulat de Hammond, c'est lui qui
est formé majoritairement.
H
H
2)
HHH
Carbocation majoritaire, car le plus substitué. Carbocation majoritaire, car le plus substitué.
E
q
u
i
l
i
b
r
e
s
d
e
p
r
o
t
o
n
a
t
i
o
n
e
t
d
e
d
é
p
r
o
t
o
n
a
t
i
o
n
: