Lois normales au Baccalauréat STMG

Lois normales au Baccalauréat STMG
Exercice 1
Partie A
Après réalisation d’une enquête, on estime
que le temps en minutes, consacré
quotidiennement par un élève à faire ses
devoirs scolaires, est une variable aléatoire
X suivant une loi normale, d’espérance 60
et d’écart type 15.
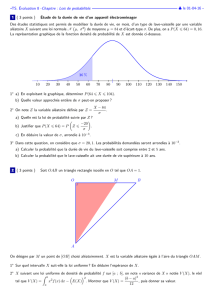
L’allure de la courbe de densité de cette loi
normale est représentée ci-dessous.
L’égalité P(X ≤ 40) = 0,0912 est illustrée
graphiquement.
1. La probabilité qu’un élève consacre quotidiennement plus de 80 minutes à faire ses devoirs scolaires est :
a. 0,0912 b. 0,8076 c. 0,8 d. 0,9088
2. La probabilité qu’un élève consacre quotidiennement moins d’une heure à faire ses devoirs scolaires est :
a. 0,5 b. 0,6 c. 1 d. 0,1368
Exercice 2 (Pondichéry, avril 2016)
(...)
4. Une machine fabrique plusieurs milliers de ces jetons par jour. On désigne par X la variable aléatoire qui, à
chaque jeton, associe son diamètre en millimètres.
On admet que X suit la loi normale d’espérance 20 et d’écart – type 0,015. Les jetons sont acceptables si leurs
diamètres appartiennent à l’intervalle [19,98; 20,02].
Calculer la probabilité qu’un jeton pris au hasard dans la production soit acceptable, arrondie à 10
– 3
.
Exercice 3 (Centres Etrangers, juin 2015)
Un laboratoire pharmaceutique fabrique des gélules contenant une substance S. La masse de substance S,
exprimée en milligrammes (mg), contenue dans une gélule est modélisée par une variable aléatoire X suivant la
loi normale d’espérance 8,2 et d’écart type 0,05.
La norme de fabrication impose que la masse de substance S dans une gélule soit comprise entre 8,1 mg et 8,3
mg. Calculer la probabilité qu’une gélule soit hors norme après la fabrication.
Exercice 4 (Antilles–Guyane, juin 2015)
(...)
Partie B
Une entreprise est composée de 1200 techniciens et de 800 ingénieurs.
On modélise le salaire mensuel, exprimé en euros, d’un technicien de l’entreprise par une variable aléatoire X
T
suivant une loi normale d’espérance m
T
et d’écart type 200.

On modélise le salaire mensuel, exprimé en euros, d’un ingénieur de l’entreprise par une variable aléatoire X
I
suivant une loi normale d’espérance m
I
et d’écart type 150.
On donne ci-dessous la représentation graphique des fonctions de densité des variables X
T
et X
I
.
1. Déterminer graphiquement m
T
et m
I
.
2. Donner une valeur arrondie au centième de p(X
T
≤ 1600).
3. En déduire une estimation du nombre de techniciens dont le salaire mensuel est inférieur ou égal à 1600.
Exercice 5
Partie B
Une des attractions du parc, une descente de type rafting dans des bouées géantes, attire beaucoup de visiteurs.
Les normes de sécurité imposent que le bassin d’arrivée contienne un volume d’eau compris entre 150 et 170
m3 d’eau. Chaque soir, à la fermeture du parc, l’équipe de maintenance effectue des vérifications et décide, ou
non, d’intervenir. Le volume d’eau (exprimé en m3) contenu dans le bassin, à la fin d’une journée
d’exploitation de cette attraction, est modélisé par une variable aléatoire X suivant une loi normale d’espérance
µ = 160 et d’écart type σ = 5.
1. a. Calculer p(150 ≤ X ≤ 170).
b. En déduire la probabilité que l’équipe de maintenance soit obligée d’intervenir pour respecter les normes de
sécurité.
2. Quelle est la probabilité que l’équipe de maintenance soit obligée, pour respecter les normes, de rajouter de
l’eau dans le bassin à la fin d’une journée d’ouverture ?
Exercice 6 (Métropole – La Réunion, septembre 2015)
(...) Partie B
On considère que désormais le taux S de satisfaction des personnes ayant téléphoné aux centres d’appel suit une
loi normale d’espérance µ = 38,2 et d’écart–type σ = 4,9.
On arrondira les résultats à 0,01 près.
1. Calculer la probabilité que le taux S de satisfaction soit compris entre 28,4 % et 48 %.
2. Calculer la probabilité que le taux S de satisfaction soit supérieur à 40 %.

Exercice 7
L’entreprise SAPIQ commercialise des pots de moutarde de 800 g.
Un pot est déclaré « conforme» s’il contient entre 790 g et 810 g de moutarde.
(...)
Partie B
L’entreprise SAPIQ reçoit un agent commercial vantant les mérites d’une nouvelle machine. La masse de
moutarde contenue dans un pot produit par cette nouvelle machine est modélisée par une variable aléatoire X.
On admet que X suit une loi normale de moyenne 800 et d’écart type 6.
1. Calculer la probabilité arrondie au millième, qu’un pot produit par la nouvelle machine soit conforme. On
pourra utiliser le résultat suivant : p(X ∈ [800 ; 810]) = 0,452.
2. L’agent commercial avance l’argument suivant : « X suit une loi normale de moyenne 800 et d’écart type 6.
Cela signifie que tous les pots produits par notre machine contiennent entre 794 et 806 g de moutarde ; ils sont
donc tous conformes. »
L’argument de l’agent commercial est-il exact ? Justifier.
Exercice 8
(...) On considère que le pourcentage de visiteurs ayant effectué un achat suit une loi normale d’espérance 42 et
d’écart – type 4.
a. Calculer la probabilité d’avoir un pourcentage de ces visiteurs inférieur ou égal à 46.
b. Calculer la probabilité d’avoir un pourcentage de ces visiteurs compris entre 34 et 50
Exercice 9
(...)
Partie B
Pour l’itinéraire en train, le temps de trajet, exprimé en minutes, est modélisé par
une variable aléatoire T. On admet que T suit une loi normale de moyenne 38 et
d’écart type 2.
Le tableau ci-dessous présente les valeurs arrondies au dix–millième des probabilités de quelques évènements
pour une loi normale d’espérance 38 et d’écart type 2.
On pourra utiliser la calculatrice ou le tableau précédent.
1. Quelle est la probabilité que le temps de trajet soit inférieur à 38 minutes ?
2. Quelle est la probabilité, arrondie au centième, que le temps de trajet soit compris entre 36 et 40 minutes ?
a p(T
≤
a)
34 0, 022 8
36 0,1587
38 0,500 0
40 0,841 3
42 0,977 3