Fiche Professeur - Gradus ad Mathematicam

Intervalle de fluctuation
Fiche Professeur
Auteur : Raymond Moché
Seconde
But de l’activité : On calcule la probabilité d’un événement Edans un cas équiprobable (tirage simultané
de 2 boules dans une urne). Puis on simule 2500 de ces tirages en calculant les fréquences successives de
réalisation de Eet on constate que la dernière fréquence de réalisation de Ecalculée tombe le plus souvent
en dehors de l’intervalle de fluctuation à 95% quand on répète les calculs. Un événement de probabilité
petite (au plus 5%) se répète donc souvent, ce qui n’est pas normal (il s’agit de l’événement « la fréquence
de réalisation de En’appartient pas à son intervalle de fluctuation à 95% »). Cela amène à ré-examiner le
modèle et la simulation.
Remarque : En deuxième partie, on propose une simulation fausse du tirage au hasard de deux boules
dans une urne en faisant le pari que les élèves ne s’en rendront pas compte. Cela amène à constater qu’un
événement de probabilité faible (5%) se produit facilement. Pour le statisticien, c’est en général le signe
que le modèle est faux. Ce n’est clairement pas le cas ici : le modèle équiprobable retenu ne peut être
contesté. On espère alors qu’un élève comprendra que c’est la simulation qui est fausse et qu’il pourra
décrire l’expérience aléatoire qu’elle représente.
Niveau de difficulté de l’activité :Il n’y a pas vraiment de difficulté algorithmique (les formules utilisées
avec le tableur sont saisies d’avance). Cette activité amène à réfléchir à la validité d’une modélisation ou
d’une simulation à partir du calcul d’un intervalle de fluctuation.
Mots-clefs : Algorithmique et probabilités intervalle de fluctuation, simulation, tableur, calcul de la
probabilité d’un événement dans le cas équiprobable.
Pré-requis :
3Probabilités : Calcul de la probabilité d’un
événement dans le cas équiprobable (rapport
du nombre de cas favorables au nombre de cas
possibles) ; division euclidienne et parité.
3Algorithmique : Dérouler une formule dans
un tableur ; commandes SOMME,LIGNE().
Matériels utilisés : ordinateurs équipés du tableur
« Calc » d’OOo ou du tableur « Excel ».
Durée indicative : 1 heure
Documents utiles à télécharger :
3Fiche Élève (pdf)
3Fiche « Ifluctuation » (ods)
Déroulement de la séance : En salle informatique ; suivre la fiche Élève.
Solution :
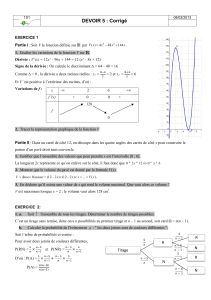
1.a - La somme a+best impaire si et seulement si aet bsont de parités différentes.
1.b - La commande =A1+B1-2*QUOTIENT(A1+B1 ;2) donne le reste de la division euclidienne de A1+B1 par
2. On sait que ce reste vaut 1 si A1 et B1 sont de parités différentes, 0 sinon (d’après la question 1.a). En
conclusion, le contenu de la case C1 vaut 1 si Eest réalisé, 0 sinon.
1.c - Saisir en E3 la formule =SOMME(C1 :C45) et exécuter. On obtient NF=25.
1.d - P(E) = 25
45 ≈0,556.
3.a - La commande LIGNE() est le numéro de la ligne courante. La commande saisie en D1 calcule donc la
fréquence de réalisation de Eaprès le premier tirage. Quand on la déroulera, elle calculera cette fréquence
du premier tirage jusqu’au tirage courant.
3.b - Au dernier calcul effectué, nous avons obtenu f= 0.589 (c’est un résultat aléatoire car il est calculé
1

à partir des résultats des tirages au hasard.
4 - L’intervalle de fluctuation à 95% , lui, n’est pas aléatoire : c’est [p−1
√2500 , p+1 √2500] = [0.536 ,0.576].
5 - On constate que fn’appartient pas à cet intervalle, ce qui est inattendu car l’événement « La fréquence
de réalisation de Eau bout de 2500 tirages appartient avec une probabilité au moins égale à 95% à
l’intervalle de fluctuation à 95% » a une grande probabilité. C’est d’autant plus inattendu que ce fait se
reproduit quand on recommence les calculs.
6 - En fait, ce que nous avons simulé n’est pas le tirage au hasard de deux boules dans l’urne. Voici le
protocole expérimental que nous avons simulé :
3on tire une boule au hasard dans l’urne ;
3puis on retire de l’urne toutes les boules, s’il y en a, dont le numéro est plus petit que le numéro de
la boule tirée et on tire la deuxième boule que l’on doit tirer parmi les boules restantes.
Vérifions que ce jeu ne se traduit pas par un modèle équiprobable, ce qui prouvera que la simulation est
fausse. En effet, si par exemple on tire d’abord la boule numéro 1 (la probabilité de cet événement est
nécessairement 1
9), il reste 9 boules pour le deuxième tirage. Ces boules étant indistinguables au toucher, les
probabilités de tirer (1,2) ou (1,3) . . . , ou (1,10) sont nécessairement égales dans tout modèle raisonnable.
Leur somme étant 1
9(additivité de la probabilité), la probabilité de tirer (1,2), par exemple, est donc 1 89·
Mais la probabilité de tirer (9,10) est la probabilité de commencer par tirer la boule numéro 9, soit 1
9,soit
une probabilité 9 fois plus grande.
La probabilité de l’événement Edans ce nouveau jeu aléatoire n’est pas 25
45 mais 1699 2835 ≈0,599 (calcul
facile et fastidieux). Dans ce cas, l’intervalle de fluctuation correct est [0.579 ,0.619].fappartient bien à
cet intervalle ; tout est normal.
Complément : Le tableur produit le graphe aléatoire de l’évolution de la fréquence des réalisations de E
au cours des 2500 tirages qui n’était pas demandé. À notre avis, ce graphe est plus parlant qu’un intervalle
de fluctuation et montre bien qu’il y a une anomalie.
Pour aller plus loin : On pourrait se demander comment simuler avec le tableur le vrai tirage simultané
au hasard de deux boules dans l’urne. La première feuille du classeur (P(E)) montre qu’il suffit de tirer
une ligne au hasard entre 1 et 45 et de lire le couple de boules tirées sur les deux premières cases de cette
ligne. Ensuite, quand on se demande si ce tirage réalise ou non l’événement E, on est amené à programmer
le tableur, sauf erreur. C’est un inconvénient désagréable des tableurs. Le même problème peut être traité
avec un logiciel de calcul, si l’avancement des élèves dans ce domaine le permet.
Références :
Intervalle de fluctuation (Examen critique des conditions n>25,0.26p60.8nécessitées par
l’utilisation d’un intervalle de fluctuation)
http://gradus-ad-mathematicam.fr/Lexique.htm
Programme de mathématiques pour la classe de seconde
http://media.education.gouv.fr/file/30/52/3/programme_mathematiques_seconde_65523.pdf