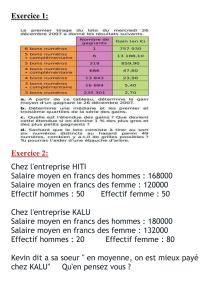
DEVOIR 5 : Corrigé

1S1
EXERCICE 1
Partie I : Soit V
la fonction définie sur
1.
Etudier les variations de la fonction
Dérivée : V’(x) = 12x² – 96x + 144
= 12 (
Signe de la dérivée :
On calcule le discriminant
Comme ∆
> 0 , la dérivée a deux racines réelles
Et V’
est positive à l’extérieur des racines, d’où
Variations de f :
2.
Tracer la représentation graphique de la fonction
Partie II
: Dans un carré de côté 12, on découpe dans les quatre angles des carrés de côté
patron d’un pavé droit sans couvercle.
1.
Justifier que l’ensemble des valeurs que peut prendre
La longueur 2x représente ce
qu’on enlève sur le côté, il faut donc que
2.
Montrer que le volume du pavé est donné par la formule
(12 2 ) (12 2 ) ... ( )
V Base Hauteur x x x V x
= × = − × − × = =
3.
En déduire qu’il existe une valeur de
V est maximum lorsque x = 2
; le volume vaut alors 128 cm
EXERCICE 2:
1. a. Soit Ω
l'ensemble de tous les tirages. Déterminer le nombre de tirages possibles.
C’est un tirage sans remise, donc on a
n
b. Calculer
la probabilité de l'événement
Soit l’arbre de probabilités ci-contre :
Pour avoir deux jetons de couleurs
différentes
P(RN) = et P(NR) =
D’où : P(A) =
P(A) =
x –∞
f '(x)
+ 0
f
Tirage
DEVOIR 5 : Corrigé
la fonction définie sur
R par
3 2
( ) 4 48 144V x x x x= − + .
Etudier les variations de la fonction
V sur R.
= 12 (
x² – 8x + 12)
On calcule le discriminant
∆ = 64 – 48 = 16
> 0 , la dérivée a deux racines réelles
: x
1
= = 2 et x
2
= = 6
est positive à l’extérieur des racines, d’où
:
Tracer la représentation graphique de la fonction
V
: Dans un carré de côté 12, on découpe dans les quatre angles des carrés de côté
Justifier que l’ensemble des valeurs que peut prendre
x est l’intervalle [0 ; 6].
qu’on enlève sur le côté, il faut donc que
0 2 12 0 6
x x
≤ ≤ ⇔ ≤ ≤
Montrer que le volume du pavé est donné par la formule
V(x).
(12 2 ) (12 2 ) ... ( )
V Base Hauteur x x x V x
= × = − × − × = =
.
En déduire qu’il existe une valeur de
x
qui rend le volume maximal. Que vaut alors ce volume
; le volume vaut alors 128 cm
3
.
l'ensemble de tous les tirages. Déterminer le nombre de tirages possibles.
n
possibilités au premier tirage et n –
1 au second, soit card
la probabilité de l'événement
A
: " les deux jetons sont de couleurs différentes ".
différentes
,
2 6 +∞
+ 0
– 0 +
128
0
5
5
R
R
N
N
R
N
08/02/2013
: Dans un carré de côté 12, on découpe dans les quatre angles des carrés de côté
x pour construire le
0 2 12 0 6
x x
≤ ≤ ⇔ ≤ ≤
qui rend le volume maximal. Que vaut alors ce volume
?
l'ensemble de tous les tirages. Déterminer le nombre de tirages possibles.
1 au second, soit card Ω =
n(n – 1).
: " les deux jetons sont de couleurs différentes ".
4
1
6
1
5
1
n
5
1

2. Le joueur gagne 2 euros s'il réalise A et perd 1 euro dans le cas contraire.
On note
X
le gain algébrique du joueur.
2. a. Donner la loi de probabilité de
X
et calculer E(X).
x
i
–1 2
P(X = x
i
)
5
×
4
−
1
+
−
5
×
−
6
−
1
=
−
11
+
50
(
−
1
)
10
−
50
(
−
1
)
D’où : E(X) = –1 ×
()
+ 2 ×
()
=
()
=
()
b. Déterminer la composition de l'urne pour que le jeu soit équitable. Conclure.
Il faut, pour que le jeu soit équitable, que E(X) = 0. Ce qui équivaut à :
– n² + 31n – 150 = 0 : ∆ = 31² – 4×(–1)×(–150) = 361
Le discriminant est positif, donc l’équation a deux solutions distinctes : = 25 et = 6.
Or le déroulement de l’expérience aléatoire impose d’avoir au moins 7 boules dans l’urne (5 rouges et 2 noires).
Conclusion : L’urne contient 25 boules.
3. a. Étudier les variations de la fonction
f
définie sur
[
[
5 ;
+∞
par
( )
2
5
10 x f x
x x
−
=
−
.
Dérivée : 
()= 10
²()()
( )²
= 10
²
( )²
Signe de la dérivée : Le dénominateur est strictement positif dans [5 ;+∞[, on étudie alors le signe de –x² + 10x –5.
∆ = 10² – 4×(–1)×(–5) = 80, les racines du numérateur sont 5 + 2√5 et 5 – 2 √5.
() est négative à l’extérieur des racines, d’où le tableau de variations :
b. En déduire la ou les valeur(s) de
n
pour la quelle le joueur a le plus de chances de réaliser A. Préciser la
probabilité correspondante.
On cherche les images par f des deux entiers les plus proches de 5 + 2√5, c'est-à-dire 9 et 10.
f(10) = ≃ 0,556 et f(9) =
"
=
Conclusion : Si l’urne contient 9 ou 10 boules, la probabilité maximale de l’événement A sera atteinte
et P(A) = ≃ 0,556
x 5 5 + 2
√
5
+∞
(
)
'
f x
+
0
−
f
√
√
0 0