Suites et récurrence DS 1

Lycée Marie Reynoard
TS
année 2015-2016
Nom : …...........................................
DS n°1
Calculatrice autorisée – Barème indicatif
Exercice 1 (12 points)
3 x− 1
x+ 1
On considère la suite définie pour tout n∈ ℕ par : u 0 = 4 et un+1 = f (un)
Soit f la fonction définie sur l’intervalle ]−1 ; +∞[ par : f ( x )=
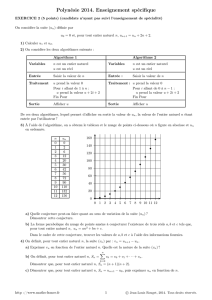
1. On a tracé, ci dessous, la courbe C représentative de la fonction f .
a) Placer sur l’axe des abscisses, u0, u1, u2 et u3. Faire apparaître les traits de construction.
b) Que peut-on conjecturer sur le sens de variation de la suite (un) ?
2. a) Montrer que la fonction f est croissante sur [0 ; +∞[.
b) Démontrer par un raisonnement par récurrence que pour tout entier naturel n, on a : 1≤ un+1 ≤ un.
En déduire le sens de variation de la suite (u n ) .
c) Justifier que la suite (u n ) est bornée
y
3
2
1
-3
-2
-1
0
-1
-2
-3
1
2
3
4
5
x
Lycée Marie Reynoard
TS
année 2015-2016
3.
Variables
U : nombre réel
N : entier naturel
Initialisation
U prend la valeur 4
N prend la valeur 0
Traitement
Tant que U – 1 > 0,5 Faire
U prend la valeur (3U-1)/(U+1)
N prend la valeur N+1
Fin tant que
Afficher N
a) Faire fonctionner cet algorithme en complétant les différentes valeurs prises par les variables
dans le tableau ci dessous (toutes les colonnes ne sont pas forcément nécessaires) :
Valeurs
initiales
U
N
U–1
b) Quelle valeur affiche l'algorithme ? Que fait cet algorithme ?
Exercice 2 (8 points)
1
Soit (un) la suite définie par u 0=1 et, pour tout entier naturel n, u n+1= u n +3 .
4
1. Calculer u 1 et u 2 .
2. Démontrer par récurrence que, pour tout entier naturel n, u n⩽ 4 .
3. Démontrer que la suite (un) est croissante.
Aide : penser à calculer u n+1− u n et à utiliser le 2.
4. Soit la suite (v n ) définie, pour tout entier naturel n, par v n =u n− 4
a) Démontrer que la suite (v n ) est géométrique. Déterminer sa raison et son premier terme.
()
n
b) En déduire que, pour tout entier naturel n, u n=− 3
1
+4
4
n
5. Soit S n la suite définie pour tout entier n par S n = ∑ u k =u0 +u 1 +...+u n
k=0
( 14 ) + 4 n .
n
Démontrer que S n=