Repères dans un plan et coordonnées d`un point

Repères dans un plan
et coordonnées d’un point
I. Repères dans un plan
Trois points d’un plan (O, I, J) définissent un repère :
Pour cela on trace les droites graduées (OI) et (OJ) telles que
- Le point O est l’origine du plan.
- Les longueurs OI et OJ définissent l’unité de chaque droite graduée.
Dans ce repère, tout point du plan est caractérisé par ses coordonnées :
- L’abscisse est le nombre projeté sur la droite (OI).
- L’ordonnée est le nombre projeté sur la droite (OJ)
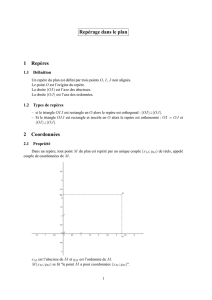
Exemple :
Les coordonnées du point C sont (-2 ; 3,5),-2 est l’abscisse et 3,5 est l’ordonnée du point C
Cas particuliers :
Si (OI) et (OJ) sont perpendiculaires, le repère est dit orthogonal.
Si OI = OJ, le repère est dit normé.
Si un repère est orthogonal et normé, on dit qu’il est orthonormé.

Placer des points sur le repère orthonormé
Créer un repère orthonormé avec la carré ABCD , puis trouver les
coordonnées des 6 points du dessin
II. Coordonnées du milieu d’un segment.
Soit (O, I, J) un repère du plan.
Soit A(xA ; yA) et B(xB ; yB) deux points quelconques de ce plan.
Soit M le milieu du segment [AB].
Les coordonnées de M sont :
;
2 2
A B A B
x x y y + +
 ÷
Exemple :
A ( 4 ; 2) et B (-2 ; 1)
Les coordonnées du milieu M
du segment [AB] sont :
M
4 ( 2) 2 1 2 3 3
; ; ; 1 ;
2 2 2 2 2 2 2
A B A B
x x y y + + + − +
= = =
 ÷  ÷  ÷ ÷      
III. Distance entre deux points.
Soit (O, I, J) un repère orthonormé du plan.
Soit A(xA ; yA) et B(xB ; yB) deux points quelconques de ce plan.
La longueur du segment [AB] est :
AB ( )² ( )²
B A B A
x x y y = − + −
Exemple :
A ( 4 ; 2) et B (-2 ; 1)
AB ( )² ( )²
B A B A
x x y y = − + −
AB ( 2 4)² (1 2)² = − − + −
AB 36 1 37 6,1 = + = ≈

Exercices :
Ex1 : Dans le triangle ABC du I) , démontrer que le triangle ABC est rectangle ?
Calculer les coordonnées des points I et J des segments [BC] et [AB]
Que peut on conclure ?
Ex 2 :
Montrer de 2 façons différentes que
EFGH est un parallélogramme.
Ex 3 : Exercices avec transformations : Symétries axiales ou centrales …....
Que remarque t-on au niveau des coordonnées.
IV. Droites.
1) Définition et équation de droite :
Une droite est un ensemble de points alignés.
Un point et une direction suffisent pour définir une droite.
Exemple : dans un plan muni d’un repère orthonormé (O, I, J)
La droite (d) passe par le point A (0 ; 3)
avec un coefficient égal à (-2).
L’équation de cette droite est
y = -2x + 3
Un point M(xM ; yM) appartient à cette
droite, si et seulement si yM = -2xM + 3

Remarque :
Correspondance avec le cours sur les fonctions affines de la forme
f(x) = ax +b et qui sont représentées par une droite dont les points ont la
forme (x;f(x))
On dira que toute droite a pour équation y = ax + b
a est la pente de cette droite et y est l'ordonnée à l'origine.
Rappel : Formule pour trouver « a » vu dans chapitre F2
Cas particulier :
Si la droite est parallèle à l’axe des abscisses,cela veut dire que la pente est nulle
son équation est de la forme y = k
Si la droite est parallèle à l’axe des ordonnées
son équation est de la forme x = k
Exercices :
•A(3;4) B(2,0) Equation de la droite (AB)
•C(4;1,4) D(0,4 ; -2) Equation de la droite (CD)
2) Droites parallèles :
Deux droites sont dites parallèles lorsqu’elles ont le même
coefficient directeur.
Si deux droites d’un plan ne sont pas parallèles,
alors elles sont sécantes en un point unique.
Exercices :
•Soit la droite D d'équation y = 2x -4 , et D' droite // à D et passant par le point
A(2 ; -3) . Trouver l'équation de D'
•Chercher l'équation de la droite D'' parallèle à D et passant par l'Origine
•Soit la droite d d'équation x = -3 . Chercher les coordonnées du point
d'intersection avec la droite D .
•B( -5 ; 2) C( -3 ; 4) D( 0 ;-3) E( 4;1) Calculer les coordonnées du
point d'intersection des droites (BC) et (DE)
Sesamath seconde Magnard
milieux : 14, 15 et 16 p 191
distance : 18, 19 p 191 22 et 23 p 192
27, 28 p 192 30 et 31 p 193
33, 34 et 35 p 194