Exercices sur les 2 premiers principes de la thermodynamique 1. 1

Exercicessurles2premiersprincipesdelathermodynamique
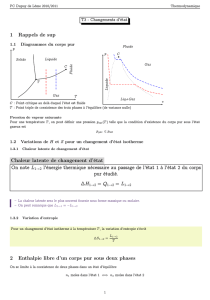
1. 1kgd'eauà20°Cdevientdelavapeurd'eauenbouillantàtempératureconstanteàla
pressionatmosphériquep=1,013.105Pa.
a. Calculerlevolumedevapeurd'eauobtenuà100°Cenadmettantqu'ellesecomporte
commeungazparfait.
b. Calculerlavariationd'énergieinternedel'eau.
Ondonnelachaleurlatentedevaporisationdel’eauLV=2,256.106J.kg‐1etsachaleur
massiquec=4180J.kg‐1.°C‐1.
2. Ungazparfaitmonoatomiqueestinitialementàlapressionp=5patmetàlatempérature
de127°C.Ilsubitunedétenteadiabatiquetellequesonvolumedouble.Calculersa
nouvellepressionetsanouvelletempérature.
3. UnmoteurfonctionnantsuivantuncycledeCarnotprendunechaleurde2.000Jàune
sourceà230°Cetredonnedelachaleuràunesourcefroideà20°C.Calculerlachaleur
donnéeàlasourcefroide,letravaildumoteuretlerendementducycle.
4. 0,2moledegazparfaitdiatomique(γ=1,4)suituncycledeCarnotentre2sourcesl'uneà
130°Cetl'autreà20°C.Sapressioninitialeestde106Paetsonvolumedoubledurantla
détenteisotherme.calculerlapression,levolume,lachaleuréchangée,letravailéchangé,
lavariationd'énergieinterne,lavariationd'entropiedurantchaqueétapeducycleetson
rendement.
5. Onporte1kgdeglacede0°Cà90°C.Calculersavariationd'entropie.
OndonnelachaleurlatentedefusionLf=3,34.105J.kg‐1etlachaleurmassiquemoyennede
l'eauc=4180J.kg‐1.°K‐1.
6. Unblocde1kgd'aluminiumà100°Cestplongédans0,5ld'eauà20°C.Calculerla
températurefinaleetlavariationd'entropiedusystème.
Ondonnelachaleurmassiquedel'aluminiumc=910J.kg‐1.°C‐1.
7. ExtraitBTS1998
1. Alatempératurede912°Csouslapressionde1bar,lefersubitunetransformation
allotropiquequilefaitpasserlorsduchauffaged'uneformenotéeFeαdestructure
cubiquecentréàuneformenotéeFeγdestructurecubiqueàfacescentrées.
PourchacunedesdeuxformesFeαetFeγ:
1.1.Dessinerlamailleélémentaire.
1.2.Préciserlenombrend'atomesdefercontenusenpropredanslamaille.
2.Lamassevolumiquepd'unmétalpeutêtredéterminéeàpartirdelarelation:
avecMlamassemolaireatomiquedufer,nlenombred'ionsoud'atomespar
mailleélémentaire,NAlaconstanted'Avogadro6,023.1023mol‐1 et a l’arêtedelamaille.
2.1.Etablirlarelationprécédente.
2.2.Calculerlesvaleursnumériquesραetργdesmassesvolumiquesà912°Cde
chacunedesformesallotropiquesdufer.Exprimerlerésultatenkg.m‐3avec4
chiffressignificatifs.
Ondonne:a(Feα)=0,2903nmeta(Feγ)=0,3646nm;M=55,85g.mol‐1.

3.Onconsidèreunemassemdefersubissantlatransformationdécriteplushaut.Cette
transformationestisothermeetisobare.Lavariationd'enthalpielibredGaucoursdela
transformationesttelleque:dG=V.dp‐S.dT.
3.1.Préciserlasignificationdestermes«isotherme»et«isobare».
3.2.Quepeut‐ondirededGetdeGaucoursdelatransformation?
3. OnenvisagelatransformationallotropiquedelamassemàunetempératureT+dT
etàpressionp+dp.LesvariationsdGαetdGγdesfonctionsGαetGγsontégales.
4.1.Endéduireque:Sγ‐Sα=(Vγ‐Vα)
4.2.Pourlatransformationréversibleenvisagée,effectuéeàtempérature
constanteT0,lavariationd'entropiedusystèmeestliéeàlaquantitéde
chaleuréchangéeaveclemilieuextérieurpar:Q=mL=T0(Sγ‐Sα)
DéfinirlachaleurlatentedetransformationallotropiqueLetpréciserson
unitéSI.
4.3.MontrerquepourlatransformationdelamassemàlatempératureT0,ona:
4.4.Sachantquelachaleurlatentedelatransformationα→γvaut15,0kJ.kg‐1,
quepγ=7653kg.m‐3etqueρα=7581kg.m‐3,déterminerlavaleur
numériquede
àlatempératureT0(enK)delatransformation.Discuter
del'effetdelapressionsurlavaleurdelatempératuredelatransformation
allotropiquedufer.