Lois de probabilités continues

N. Duceux – Lycée Paul Doumer – Année 2012/13 Page 1
Lois de probabilité continues
Lois à densité sur un intervalle
𝐿𝑒𝑠𝑒𝑥𝑝é𝑟𝑖𝑒𝑛𝑐𝑒𝑠𝑎𝑙é𝑎𝑡𝑜𝑖𝑟𝑒𝑠é𝑡𝑢𝑑𝑖é𝑒𝑠𝑒𝑛𝑝𝑟𝑒𝑚𝑖è𝑟𝑒𝑐𝑜𝑛𝑑𝑢𝑖𝑠𝑎𝑖𝑒𝑛𝑡à𝑑é𝑓𝑖𝑛𝑖𝑟𝑢𝑛𝑢𝑛𝑖𝑣𝑒𝑟𝑠
𝛺={𝜔;𝜔;…;𝜔}fini munid’uneloideprobabilitéPquiattribuaitàchaqueissue𝜔 sa
𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡é𝑃(𝜔)𝑡𝑒𝑙𝑙𝑒𝑞𝑢𝑒𝑃(𝜔)≥0𝑒𝑡∑𝑃(𝜔)=1.
ToutevariablealéatoiredéfiniesurΩneprenaitqu’unnombrefinidevaleurs.
Ons’intéressemaintenantà des univers qui contiennent une infinité d’issues, par exemple toutes valeurs
dansl’intervalle[0;1]. Les variables aléatoires utilisées sur ces univers prennent toutes valeurs dans un
intervalle donné.
Définition – Densité de probabilité
On appelle densité de probabilité sur un intervalle 𝐼 de ℝ,
toute fonction 𝑓 continue, positive sur 𝐼 et telle que l’aire
sous la courbe 𝐶 est égale à 1 u.a.
Ainsi toute fonction 𝑓 continue, positive sur 𝐼 est une
densité de probabilité si: ∫𝑓(𝑡)𝑑𝑡=1𝑠𝑖𝐼=[𝑎;𝑏]
où lim
→ f(t)dt=1siI=[a;+∞[
Définition – Loi à densité
Soit 𝑓 une densité de probabilité sur un intervalle 𝐼.
Direqu’unevariablealéatoire𝑋 suit la loi de densité 𝑓 signifiequ’àtoutintervalle𝐽 inclus dans 𝐼, on
associe la probabilité 𝑃(𝑋∈𝐽)=𝑎𝑖𝑟𝑒𝐷 où 𝐷 estledomainedel’airesouslacourbe𝐶 sur
l’intervalle𝐽.
Conséquences
 Pour tout nombre réel 𝑐 ∈𝐼, 𝑃(𝑋=𝑐)=∫𝑓(𝑡)𝑑𝑡 =
0
 Si 𝐽=[𝑐;𝑑], 𝑃(𝑋∈𝐽)=𝑃(𝑐 ≤𝑋≤𝑑)=∫𝑓(𝑡)𝑑𝑡
 (Aire sous la courbe délimitée par
{𝑀(𝑥;𝑦)/𝑐≤𝑥 ≤𝑑et0≤𝑦≤𝑓(𝑥)}).
 𝑃(𝑐≤𝑋≤𝑑)=𝑃(𝑐<𝑋 ≤𝑑)=𝑃(𝑐≤𝑋<𝑑)=𝑃(𝑐<𝑋 <𝑑)
Propriétés
Lespropriétésdesprobabilitésrencontréesdanslecasdiscrets’étendentaucascontinu.Ainsi :
 𝑃(𝑋∉𝐽)=1−𝑃(𝑋∈𝐽) (Complémentaire).
En particulier, si 𝐼 =[𝑎;+∞[ et si 𝑐>𝑎 alors 𝑃(𝑋>𝑐)=1−𝑃(𝑎 <𝑥 <𝑐)=1−∫𝑓(𝑡)𝑑𝑡
 Si 𝐽 et 𝐾 sont deux intervalles inclus dans 𝐼,
alors 𝑃(𝑋∈𝐽∪𝐾)=𝑃(𝑋∈𝐽)+𝑃(𝑋∈𝐾)−𝑃(𝑋 ∈𝐽∩𝐾)
 Si 𝑃(𝑋∈𝐽)≠0, alors 𝑃∈(𝑋∈𝐾)=(∈∩)
(∈)
𝑃(𝑎≤𝑋≤𝑏)=1

N. Duceux – Lycée Paul Doumer – Année 2012/13 Page 2
Exemple
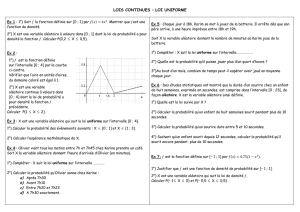
𝑓 estlafonctiondéfiniesurl’intervalle[0;4] par la
courbe ci-contre :
1) Vérifierquel’aire,enunitéd’airedudomainecoloré
est égale à 1. Que peut-on en déduire pour 𝑓 ?
2) 𝑋 est une variable aléatoire continue à valeurs dans
[0;4] dont la loi de probabilité a pour densité 𝑓.
a) Calculer 𝑃(1≤𝑋≤2)
b) Calculer 𝑃(1,5≤𝑋≤2,5)
Définition – Espérance mathématique
L’espérancemathématiqued’unevariablealéatoire𝑋 dont la densité de probabilité 𝑓 est définie sur
un intervalle fermé [𝑎;𝑏] est 𝐸(𝑋)=∫𝑥𝑓(𝑥)𝑑𝑥
.
Remarque
Cettedéfinitionprolongeaucadrecontinuladéfinitiondonnéedel’espéranced’unevariablealéatoire
discrète.
Loi uniforme sur [𝒂;𝒃]
La loi uniforme est la loi de phénomènes continus uniformément répartis sur un intervalle.
Définition
Une variable aléatoire 𝑋 suituneloiuniformesurl’intervalle
[𝑎;𝑏], avec 𝑎<𝑏, lorsque sa densité de probabilité 𝑓 est une
fonction constante sur [𝑎;𝑏].
Propriété
La densité de probabilité de la loi uniforme sur [𝑎;𝑏] est la
fonction définie sur [𝑎;𝑏] par 𝑓(𝑥)=
.
Preuve
La densité de probabilité 𝑓 de la loi uniforme sur [𝑎;𝑏] est une
fonction constante.
Posons 𝑓(𝑥)=𝜆.
On doit avoir ∫𝑓(𝑥)𝑑𝑥=1
 soit ∫𝜆𝑑𝑥 =1⟺𝜆𝑏−𝜆𝑎 =1⟺𝜆=  .
𝑃(𝑐≤𝑋≤𝑑)= 𝑓(𝑡)𝑑𝑡
𝑃(𝑋>𝑐)=1−𝑃(𝑎≤𝑋≤𝑐)=1− 𝑓(𝑡)𝑑𝑡

N. Duceux – Lycée Paul Doumer – Année 2012/13 Page 3
Remarques
1. Sil’onchoisitauhasard unnombredansl’intervalle𝐼 =[𝑎;𝑏], la probabilité que ce nombre soit
dansl’intervalle𝐽⊂𝐼 est le quotient da la longueur 𝐽 par celle de 𝐼.
En effet, pour tout intervalle 𝐽=[𝛼;𝛽]⊂[𝑎;𝑏]=𝐼, 𝑃(𝑋∈𝐽)=∫
𝑑𝑡=  =
2. Si deux intervalles 𝐽et 𝐾ont la même longueur alors 𝑃(𝑋∈𝐽)=𝑃(𝑋∈𝐾).
D’oùlenomdeloiuniforme.
Exemple
Onchoisitunnombreauhasarddansl’intervalle[0;5].
Par définition la variable aléatoire 𝑋 qui indique le nombre choisi suit la loi uniforme sur [0;5].
𝑃(𝑋=2)=0 ; 𝑃(𝑋>3)=
=  ; 𝑃(1≤𝑋<4)= =
Propriété – Espérance mathématique
Soit 𝑋 unevariablealéatoirequisuitlaloiuniformesurl’intervalle[𝑎;𝑏].
Alors son espérance est 𝐸(𝑋)=
Preuve
𝐸(𝑋)=∫
𝑑𝑡= 
=
 × =  ×()() =
Exemplesd’utilisationdelaloiuniforme
1) Jeanne aditqu’ellepasseraitchezJean entre 18h et 20h30.Quelleestlaprobabilitéqu’ellearrive
pendantqu’ilmangeentre19het19h30 ?
On note 𝑋 lavariablealéatoireégaleàl’heured’arrivéedeJeanne chez Jean. Elle prend ses valeurs
dans l’intervalle[18;20,5]. 𝑋 suit une loi uniforme sur [18;20,5].
𝑃(19≤𝑋 ≤19,5)=19,5−19
20,5−18=0,2
La probabilité que Jeanne arrive pendant le repas est 
.
2) Unfeutricolorereste55secondesauvert,5secondesàl’orangeet60secondesaurouge.
Un piéton ne peut traverser que lorsque le feu est rouge. A 8h00, le feu passe au rouge.
Ons’intéresseauxpiétonsquiseprésentententre8h00et8h05.𝑇 est la variable aléatoire qui donne,
enseconde,letempsécouléde8h00jusqu’àl’heured’arrivéedevantlefeu d’unpiétondésirant
traverser. On suppose que 𝑇 suit la loi uniforme [0;300].
Onveutcalculerlaprobabilitéqu’unpiétonattendemoinsde10secondespuisplusde20secondes.
a) Faire un schéma illustrant la succession des feux.
b) Pour une attente de moins de 10 secondes, dans quels intervalles de temps doit se situer T ?
Une attente de moins de 10 secondes signifie que 𝑇∈[0;60] ou 𝑇 ∈]110;180] ou 𝑇∈]230;300].

N. Duceux – Lycée Paul Doumer – Année 2012/13 Page 4
Endéduirelaprobabilitéquel’attentenedépassepas10 secondes.
Les évènements 𝑇∈[0;60], 𝑇∈]110;180], 𝑇∈]230;300] sont deux à deux disjoints donc
𝑃(𝑇∈[0;60] ∪]110;180] ∪]230;300])=𝑃(𝑇∈[0;60])+𝑃(𝑇∈]110;180])+𝑃(𝑇∈]230;300])
𝑃(𝑇∈[0;60] ∪]110;180] ∪]230;300])= 
+ +  =
c) Calculerlaprobabilitéquel’attentedureplusde20secondes.
Une attente de plus de 20 secondes signifie que 𝑇∈]60;100[ ou 𝑇∈]180;220[.
Ces évènements sont deux à deux disjoints donc
𝑃(𝑇∈]60;100[ ∪]180;220[)=𝑃(𝑇∈]60;100[)+𝑃(𝑇∈]180;220[)=
+  =
3) La fonction Rand ou NbrAléat sur TI ou Ran#surCasiod’unecalculatrice donne un nombre au
« hasard »dansl’intervalle[0;1[. Ce nombre aléatoire suit la loi uniforme 𝑋 sur [0;1[. Par exemple la
probabilité que 𝑋∈0;
 est  . Plus généralement, si 𝑎 et 𝑏 sont deux nombres tels que 0≤𝑎 <𝑏<1,
la probabilité que 𝑋∈[𝑎;𝑏] est 𝑏−𝑎.
a) Calculer 𝑃(0,54≤𝑋≤0,62)
𝑃(0,54≤𝑋≤0,62)=0,62−0,54=0,08
b) Sachant que 𝑋<0,3,quelleestlaprobabilitédel’évènement𝐴 : « son chiffre des centièmes est 1 ».
Les nombres inférieurs à 0,3 dont le chiffre des centièmes est 1 sont dans les intervalles [0,01;0,02[ ou
[0,11;0,12[ ou [0,21;0,22[.
𝑃,(𝐴)=(0,02−0,01)+(0,12−0,11)+(0,22−0,21)
0,3−0 =3×0,01 0,3 =1 10
c) Calculerl’espérancede𝑋.
𝐸(𝑋)=0+1
2=1 2
Lois exponentielles
La plupart des phénomènes naturels sont soumis au processus de vieillissement. Par exemple, la durée de
vie des êtres humains :laprobabilitédevivre40anspourunenfantàlanaissanceestdel’ordrede0,98.
La probabilité pour une personne de 50 ans de vivre encore 40 ans est environ égale à 0,65.
Il existe des phénomènes où il n'y a pas de vieillissement ou d'usure. Dans la pratique, ils relèvent
d'événements survenant accidentellement et/ou de façon brutale.
L’absence de « mémoire » ou de vieillissement  se traduit par le fait qu’un phénomène a autant de
chancesdeseproduiresurunlapsdetempsdonnéaprèsl’instant𝑡 qu’aprèsl’instantℎ. La probabilité
qu’il survienne aujourd’hui sachant qu’on l’attend depuis un siècle est la même que si on l’attendait
depuis un jour.
Les lois exponentielles modélisent cesphénomènesdontladuréedevien’estpasaffectéeparl’âge, par
exemple la durée de vie d’unnoyauradioactifoud’uncomposantélectronique.
Définition
𝜆 désigne un nombre réel strictement positif.
Une variable aléatoire 𝑇 suit une loi exponentielle de paramètre 𝜆 lorsque sa densité de probabilité est
la fonction 𝑓 définie sur [0;+∞[ par 𝑓(𝑡)=𝜆𝑒.

N. Duceux – Lycée Paul Doumer – Année 2012/13 Page 5
Remarque
La fonction 𝑓 définie sur [0;+∞[ par
𝑓(𝑡)=𝜆𝑒 est bien une densité de probabilité
sur [0;+∞[ :
𝑓 est continue et positive sur [0;+∞[ et si
𝑡>0,∫𝜆𝑒𝑑𝑥=
−𝑒
=1−𝑒.
Or, lorsque 𝑡tend vers +∞, 𝜆𝑡 aussi et donc 𝑒
tend vers 0. On a donc
lim
→∞ 𝜆𝑒𝑑𝑥=
 𝜆𝑒𝑑𝑥 =1
∞
Propriétés
Pour tous nombres réels 𝑎 et 𝑏 tels que
0≤𝑎 ≤𝑏 :
𝑃(𝑇≤𝑎)= 𝜆𝑒𝑑𝑡
=−𝑒
=1−𝑒
𝑃(𝑇>𝑎)=1−𝑃(𝑡≤𝑎)=𝑒
𝑃(𝑎≤𝑇≤𝑏)=𝑒 −𝑒
Théorème (Propriété de perte de mémoire)
Pour tous nombres réels positifs 𝑡 et ℎ,
𝑃(𝑇≥𝑡+ℎ)=𝑃(𝑇≥ℎ).
La durée de vie 𝑇 sur un laps de temps ℎ,nedépendpasdel’âge𝑡 à partir duquel on considère cet
évènement.
Preuve
Pour tous nombres réels positifs 𝑡 et ℎ,
𝑃(𝑇≥𝑡+ℎ)=[()∩()]
() =() () =()  =𝑒 =𝑃(𝑇≥ℎ).
Proposition – Espérance mathématique
L’espérancemathématiquedelaloiexponentielledeparamètre𝜆 est 𝐸(𝑇)=
.
Preuve (Exigible)
Pour tout nombre réel positif 𝑡, on calcule ∫𝜆𝑥𝑒𝑑𝑥
.
La fonction 𝑔:𝑥⟼𝜆𝑥𝑒 est le produit des fonctions dérivables 𝐼𝑑:𝑥 ⟼𝑥 et 𝑥⟼𝜆𝑒. Donc 𝑔 est
dérivable sur [0;+∞[.
 𝜆𝑥𝑒𝑑𝑥
=−𝑥𝑒
− −𝑒𝑑𝑥
=−𝑡𝑒 +−𝑒
𝜆
=−𝑡𝑒 −𝑒
𝜆+1 𝜆
lim
→𝑒
𝜆=0et lim
→−𝑡𝑒 = lim →1
𝜆−𝜆𝑡𝑒
Onpose𝑋=−𝜆𝑡.Alors lim
→𝑋 =−∞et
lim
→𝑋𝑒=0(𝑐𝑟𝑜𝑖𝑠𝑠𝑎𝑛𝑐𝑒𝑠𝑐𝑜𝑚𝑝𝑎𝑟é𝑒𝑠)
Onadonc lim
→ 𝜆𝑥𝑒𝑑𝑥=𝐸(𝑇)=1
𝜆