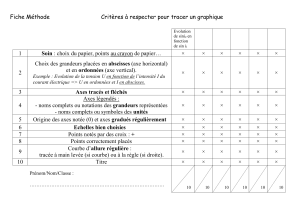
DS4 fonc 14-15

Devoir surveillé de mathématiques n°4 11 décembre 2014 2nde
Nom-Prénom :
Exercice 1:(3,5)On donne ci- contre le tableau
de variations d'une fonction
f
:
1°) Compléter :
« sur l'intervalle [-4;2], le minimum de f est ……….. atteint en ……………... »
2°) Comparer, si possible, en justifiant soigneusement (on écrira « impossible »
sinon):
a)
f(3)
et
f ( 2,5 )
……………………………………………………………
………………………………………………………………………………………
b)
f
(
3
) et
f
(
1
)……………………………………………………………
………………………………………………………………………………………
c)
f
(
1
) et
f
(
1
) ……………………………………………………………
………………………………………………………………………………………
4°) Déterminer le nombre de solutions de l'équation
f
(
x
)=
1
, et donner leur valeur
ou un intervalle auquel la solution appartient: ............................................................
.....................................................................................................................................
Exercice 2:(6) Lectures graphiques
On considère la fonction f définie sur [-3;5] donnée par
sa courbe ci-contre :
1°)Par lecture graphique
a) Déterminer l'image de 0...........
b) Déterminer les antécédents de 0................
c) Résoudre l'inéquation
f
(
x
)<
2
.
.............................……………………………………….
2°) Pour quelles valeurs de k l'équation
f
(
x
)=
k
admet une seule solution ?
………………………………………………………………..
3°) Ci-dessous :
a) Effectuer le tableau de variations de f.
b) Effectuer le tableau de signes de f.
4°) On considère la fonction g définie sur [-3;5] par
g
(
x
)=
3
x
a) Tracer sur le graphique précédent la représentation graphique de g (avec un
pas de 1.)
b) Résoudre graphiquement l'inéquation
f
(
x
)<
g
(
x
) : ...................................
Exercice 3:(5,5) On considère la fonction f(x)=2(x
2
9)( x3)(3x+5)
1°) Développer et réduire f
2°) Factoriser f (pour la suite , on pourra admettre que
f ( x )=( x 3 )( x + 1 )
)
3°) Déterminer, par le calcul, si le point A( 1
+
√
2 ; 2
√
2 2 ) appartient à la courbe
représentative de f.
4°) Calculer les coordonnées des points d'intersection de
C
f
avec l'axe des
abscisses.

Exercice 4 (5) :
Une personne est tombée en panne
avec sa voiture. Elle pousse sa voiture,
puis, arrivée en haut de la côte, elle
remonte dans sa voiture et relève la
vitesse inscrite au compteur (en km/h) en fonction du temps
écoulé (en secondes) depuis qu'elle est montée dans la voiture.
Ci-contre est représenté une partie du nuage de points de ce relevé , formant
la représentation graphique d'une fonction donnant la vitesse en fonction du temps.
1°) Par lecture graphique, répondre aux questions suivantes :
a) Quelle est la vitesse du véhicule au moment où la
personne monte à bord ? ……………………………..
b) Quelle est la vitesse maximale atteinte par le véhicule ?
……………………………………………………………..
c) Au bout de combien de temps le véhicule commence-t-il
à ralentir ? ………………………………………………..
d) Durant combien de temps la vitesse du véhicule est-elle
supérieure à 11 km/h ? Répondre et indiquer
sur le graphique ce qui vous a permis de répondre.
……………………………………………………………..
e) Expliquer pourquoi ce graphique ne nous permet pas de savoir quand le
véhicule s'est arrêté. ……………………………………………………………..
…………………………………………………………………………………….
2°) a) On considère les fonctions :
f(x)=0,5 x
2
+3x+10 g(x)=x
2
+5x+10
Laquelle de ces deux fonctions a pour représentation graphique celle donnée ci-
dessus ? Justifier.
b) En utilisant la réponse à la question précédent, déterminer par le calcul les instants où la
vitesse du véhicule est de 10km/h.
3°) En utilisant votre calculatrice, indiquez, avec une précision de 0,1 seconde, après combien
de temps le véhicule s'immobilise.

Devoir surveillé de mathématiques n°4 11 décembre 2014 2nde
Nom-Prénom :
Exercice 1:On donne ci- contre le tableau de
variations d'une fonction
f
:
1°) Compléter :
« sur l'intervalle [-4;2], le minimum de f est -5 atteint en -2 »
2°) a) -3<-2,5 et f est décroissante sur [-3 ;-2,5] donc
f
(
3
)>
f
(
2,5
)
b)
f
(
3
) est compris entre -3 et -5 et
f
(
1
) est compris entre 1 et 2 donc
f
(
3
)<
f
(
1
)
c)
f
1
 et
f
(
1
) impossible
4°)
f
(
x
)=
1
a deux solutions : une sur l'intervalle [-2;0] et l'autre égale à 2
Exercice 2:Lectures graphiques
On considère la fonction f définie sur [-3;5] donnée par
sa courbe ci-contre :
1°)Par lecture graphique
a) image de 0 : c'est 6
b) Déterminer les antécédents de 0 ce sont -2 et 3
c)
f
(
x
)<
2
: S=[-3 ;-1[ ∪ ]2;5]
2°) Pour quelles valeurs de k l'équation
f
(
x
)=
k
admet une seule solution ?
Si k ∈ [-3 ;-2[ ∪ {6}
3°) a) tableau de variations de f.
x
–3 0 5
f
(
x
)
–2
6
–3
b) tableau de signes de f.
x–3 –2 3 5
f(x) – 0 + 0 –
4°)
f
(
x
)<
g
(
x
)
: S=[-3 ;-0,5[ ∪ ]3;5]
Exercice 3:
f(x)=2(x
2
9)( x3)(3x+5)
1°) Développer et réduire f
f(x)=2(x
2
9)( x3)(3x+5)
f(x)=2x
2
18[3x
2
+5x9x15]
f(x)=2x
2
183x
2
5x+9x+15
f(x)=x
2
+4x3
2°) f(x)=2(x
2
9)( x3)(3x+5)
f
(
x
)=
2
(
x
3
)(
x
+
3
)(
x
3
)(
3
x
+
5
)
f
(
x
)=(
x
3
)[
2
(
x
+
3
)(
3
x
+
5
) ]
f
(
x
)=(
x
3
)[
2
x
+
6
3
x
5
]
f
(
x
)=(
x
3
)(
x
+
1
)
3°) f(1+
√
2)=(1+
√
2)
2
+4(1+
√
2)3
= (1+2
√
2+2)+4+4
√
23
= 12
√
22+4+4
√
23
= 2
√
22 donc A ∈
C
f
4°)
C
f
coupe l'axe des abscisses lorsque
f
(
x
)=
0
⇔
(
x
3
)(
x
+
1
)=
0
⇔
x
3
=
0
ou
x
+
1
=
0
⇔ x=3 ou x=
1
1
=1
Donc
C
f
coupe l'axe des abscisses aux points (3;0) et (1;0)

Exercice 4 :
1°) Par lecture graphique, répondre aux questions suivantes :
a) Quelle est la vitesse du véhicule au moment où la
personne monte à bord ? Elle est égale à l’image de 0 donc 10km/h
b) Quelle est la vitesse maximale atteinte par le véhicule ?
Environ 14,5 km/h
c) Au bout de combien de temps le véhicule commence-t-il
à ralentir ? Lorsque la vitesse commence à diminuer soit après 3 sec.
d) Combien de temps la vitesse du véhicule est-elle
supérieure à 11 km/h ? Répondre et indiquer
sur le graphique ce qui vous a permis de répondre.
On résout
f
(
x
)>
11
⇔ x ∈]0,5;5,5|, soit durant 5 sec.
e) Expliquer pourquoi ce graphique ne nous permet pas de savoir quand le
véhicule s'est arrêté. Il faudrait savoir quand
f
(
x
)=
0
, soit avoir l'intersection de
la courbe avec l'axe des abscisses.
2°) a)
f
(
1
)=
12,5
et
g
(
1
)=
14
donc d'après le graphique, le fonction cherchée
est f.
b)On résout
f
(
x
)=
10
⇔ 0,5 x
2
+3x+10=10 ⇔
0,5
x
2
+
3
x
=
0
⇔
x
(
0,5
x
+
3
)=
0
⇔
x
=
0
ou 
0,5
x
+
3
=
0
⇔
x
=
0
ou
x=3
0,5
=6
.
Donc la vitesse est égale à 10 km/h à l'instant initial et après 6 sec.
3°) Sur la calculatrice, on cherche graphiquement ou à l'aide de la table la valeur pour
laquelle
f
(
x
)=
0
. On trouve x ≈ 8,4.
Elle s'immobilise après 8,4 sec environ.