TES Ch8 Lois à densité

LOI DE PROBABILITE A DENSITE
I.Introduction :
1) Variables aléatoires discrètes et continues :
Si on a un shéma de Bernoulli ( n épreuves successives et indépendantes pour lesquelles la probabilité
d'un succès est p ) , la variable aléatoire X qui compte le nombre de succès suit une loi binomiale de
paramètres n et p , notée B(n,p). On sait également que :
n
P(X = k ) =  k  pk ( 1 – p )n–k ; E(X) = np ; Var(X) = np ( 1 – p ) et X = np ( 1 – p )
Dans ce cas, la variable aléatoire X ne prend qu'un nombre fini de valeurs ( le nombre de succès
possibles). On dit que cette variable aléatoire est discrète.
Lorsque la variable aléatoire est discrète, on peut remplir un tableau de ce genre :
X = xi
x1
x2
x3
…….
xn
TOTAL
P(X = xi )
p1
p2
p3
…….
pn
1
On a alors E(X) = p1  x1 + p2  x2 + p3  x3 + …. + pn  xn
et
Var(X) = ( p1  x1 ² + p2  x2 ² + p3  x3² + …. + pn  xn² ) – (E(X)) ²
X = Var(X)
Or, dans les domaines économiques et industriels, on est amené à étudier des variables aléatoires pouvant
prendre, au moins théoriquement, n'importe quelle valeur dans IR ou dans un intervalle de IR.
On dit alors que ces variables aléatoires sont continues.
X prend alors toutes les valeurs d'un intervalle de IR.
Exemple : Dans une fabrique d'ampoules, on peut s'interresser à la durée de vie en heures d'une ampoule choisie au hasard.
La variable aléatoire associée à cette durée de vie est alors continue.
Elle pourra prendre toutes les valeurs possibles entre 0 et +  !
Pour ce type de variable aléatoire , ce n'est pas la probabilité de l'événement X = 400 qui va être interressante,
mais plutôt la probabilité de l'événement X  400 ou 400  X  1000.
On ne pourra pas faire, dans le cas d'une variable aléatoire continue, de tableau comme pour les variables
aléatoires discrètes. Pour ce type de variable aléatoire, les valeurs isolées prises par les variables
aléatoires discrètes vont être remplacées par des intervalles.
Au niveau graphique, la hauteur des bâtons sera remplacée par l'aire d'une portion de plan située dans un
intervalle et au dessous d'une courbe représentative d'une fonction liée à la loi de probabilité utilisée :
la fonction de densité de la loi de probabilité .
Pour calculer la probabilité que X appartienne à un intervalle fixé, il faudra alors calculer une aire
donc le plus souvent, une intégrale.
2) Fonction densité d'une loi continue :
a) Définition :
Une fonction f définie sur IR sera une fonction de densité d'une loi continue si :
 f(x)  0 pour tout x de IR
 f est continue sur IR
 L'aire du domaine limité par la courbe représentative de f et l'axe des abscisses vaut 1.
b) Probabilité d'un événement avec une loi continue, de densité f :
ab f(x)dx
P( a  X  b) = 
c) Propriétés :
k
P(X = k ) = P( k  X  k ) = 
k f(x)dx = 0 et P(a  X  b)=P(a < X  b)=P(a  X < b)=P(a < X < b)
d) Propriétés :
i=n
E(X) =  xi P( X = xi ) pour une loi discrète. Cette définition n'a pas de sens pour une loi continue.
i=1
On prolonge cette définition par :
b
Si X est une variable aléatoire continue sur [a;b] de densité f alors E(X) = 
a x f(x)dx
II. Deux lois continues :
1) La loi uniforme :
a) Exemple :
1. a) Il y a 10 nombres ayant au plus une décimale
1
dans [0;1[ donc la probabilité est
.
10
b) Il y a 10 nombres ayant au plus deux
décimales dans [0;0,1[ donc 100 dans [0,1[
1
la probabilité est
.
100
n
c) Il y a 10 nombres ayant au plus n décimales
1
dans [0,1[ la probabilité est
.
10n
2. S'il n'a aucune indication, le nombre de
possibilités est 10n qui tend vers +  donc la
probabilité de trouver le nombre tend vers 0.
3. a) La longueur des deux intervalles est de 0,2.
La longueur de l'intervalle [0;1[ est de 1.
Donc la probabilité d'être dans un de ces deux
0,2 2 1
intervalles est la même :
= = .
1 10 5
b) La longueur du premier intervalle est 0,1,
celle du second est 0,4 donc la probabilité
d'être dans le second sera 4 fois plus
importante que d'être dans le premier.
b) Champ d'intervention de la loi uniforme :
La loi uniforme intervient à chaque fois que l'on est amené à choisir un nombre au hasard dans un
intervalle.
c) La loi uniforme sur [a;b] :
Si la variable aléatoire X suit une loi uniforme sur [a;b], sa fonction densité est définie sur IR
par :
 1 si a  x  b
f(x) =  b – a
 0 sinon
 Représentation graphique :
 Calcul d'une probabilité :
Si c et d sont deux nombres de l'intervalle [ a ; b ]
d 1
1
d–c
P( c  X  d ) = 
 b – a dx = b – a ( d – c ) = b – a
c
b
1
1
b² – a² a + b
b x dx = 1
 Espérance de X : E(X) = 
=
 x  b – a dx = b – a 

a
b–a
2
2
a
2) Passage de la loi binomiale à la loi normale :
Exemple : Dans un club de sport, Julien joue au basket. Il sait que, lors d'un lancer, sa probabilité de
marquer un panier est de 0,6. Julien lance n fois de suite la ballon en direction du panier.
Les n lancers sont indépendants les uns des autres.
X est la variable aléatoire qui compte le nombre de paniers marqués.
1) Montrer que X suit une loi binomiale dont on précisera les paramètres.
On a n lancers successifs et indépendants. On appelle succès l'événement S " marquer un panier ".
P(S) = 0,6 . X est la variable aléatoire qui compte le nombre de succès.
Elle suit donc une loi binomiale de paramètres n et 0,6.
2) Etablir la loi de probabilité de X pour n = 4 et n = 10.
X = xi
0
1
2
3
4
Total
P(X = xi )
 4   ( 0,6)0  (0,4)4 =
0
0,0256
0,1536
0,3456
0,3456
0,1296
1
Avec la calculette, on tape 2nde VARS puis A:binomFdp(nombre d'essais,probabilité succès,xi )
X = xi
P(X = xi )
0
1.10–4
1
0,0016
2
0,0106
3
0,0424
4
0,1115
5
0,2007
6
0,2508
7
0,215
8
0,1209
9
0,0403
10
0,006
3) Représenter à l'aide d'un histogramme chacun de ces deux cas.
Animation geogebra : binomiale_observation.ggb
4) Calculer E(X) et X .
Pour n = 4
E(X) = np = 4  0,6 = 2,4 ;  = np(1–p) = 2,4  0,4 = 0,96 0,98
Pour n = 10 E(X) = np = 10  0,6 = 6 ;  = np(1–p) = 6  0,4 = 2,4 1,55
Total
1
Sur chacun des diagrammes en bâtons, je vais tracer la courbe représentative de la fonction f définie par :
1 x– 2
1
f(x) =
e – 2    . avec  représentant l'espérance ou la moyenne .
 
 2
Donc pour n = 4 on trace f4(x) =
et pour n = 10 on trace f10(x) =
1
0,96 
1
e –2
2

x – 2,4 2
0,96


 = 2,4 et  = 0,96
1 x–6 2
1
e – 2  2,4 avec  = 6 et  = 2,4
2,4  2 
 
Animation geogebra : BinomialeApproxNormale.ggb
On observe que la courbe passe presque par les sommets de chaque bâton.
On admettra que si n est assez grand, si p n'est pas trop voisin de 0 ou de 1, la loi binomiale de paramètres n et
p peut être approchée par une loi dite loi normale, de paramètres  = np et  = np(1–p).
Cette loi sera notée N( ,² ) ou N(  ,  ) sur certains livres.
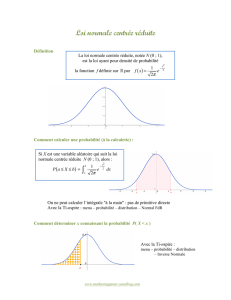
3) La loi normale :
La loi normale N(  , ² ) est une loi de probabilité continue dont la densité est
1 x– 2
1
f(x) =
e – 2    . Ces paramètres sont  = E(X) et  ( écart–type ). Donc Var(X) = ²
 
 2
Remarques :
 f est continue sur IR et f(x)  0 pour tout x de IR
 L'aire du domaine limité par la courbe représentative de f et l'axe des abscisses vaut 1.
 Champ d'intervention de la loi normale :
Elle intervient dans la modélisation de phénomènes aléatoires possédant de nombreuses causes
indépendantes, dont les effets s'ajoutent sans que l'un soit prédominant. Etant donné la complexité des
phénomènes économiques, sociaux ou naturels, elle intervient dans la plupart des phénomènes
aléatoires d'où son nom.
 Rôle de  et  sur la courbe de la fonction densité de la loi normale :
a) Rôle de  :
La courbe se centre sur la droite d'équation x = .
b) Rôle de  :
Plus  augmente, plus l'ordonnée du sommet est petite et plus l'intervalle autour de  est large.
Le sommet de la courbe a pour coordonnées (  ; f () ) avec f(x) =
donc (  ;
1

2
).
1

2
diminue quand  augmente .
Animation geogebra : B Effet de mu et de sigma.ggb
1 x– 2
e –2

 2
1



 Cas particulier : la loi normale centrée réduite : N( 0 , 1 ):
Que signifie centrer et réduire une variable aléatoire et quel est l'intérêt de cette technique ?
Reprenons l'exemple de la variable aléatoire X suivant une loi binomiale B(n,p)
Posons Y la variable aléatoire définie par Y = X – E(X)
Cette variable aléatoire aura une moyenne de 0.
Au niveau du graphique, on constate que celui-ci se centre sur l'axe des ordonnées.
Animation geogebra : binomiale_centree.ggb
On dit que l'on a centré la variable aléatoire X.
X – E(X)
.
X
Cette variable aléatoire a une moyenne de 0 et une variance de 1 donc un écart–type de 1.
Au niveau du graphique, on constate que celui-ci se resserre autour de l'axe des ordonnées.
En effet, l'écart-type est plus petit.
Posons Z la variable aléatoire définie par Z =
Animation geogebra : binomiale_centree_reduite.ggb
On dit que l'on a centré et réduit la variable aléatoire X.
Lorsque l'on fait le même travail avec une variable aléatoire X suivant une loi normale de paramètres
X–
 et , on obtient une variable Z=
qui suit une loi normale de paramètres  = 0 et  = 1 .

Cette loi est la loi normale centrée réduite N( 0 , 1 ) .
x²
1
La fonction densité de cette loi est plus simple : f(x) =
e–2 .
2
Pour étudier les lois normales, il suffit donc de bien connaitre la loi normale centrée réduite.
Représentation de la loi normale centrée réduite :
 Calcul d'une probabilité avec la loi normale :
b
P( a  X  b ) = 
a f(x)dx
avec
f(x) =
1

1 x– 2
e –2

2

 .

Nous ne savons pas calculer cette intégrale en TES donc nous nous servirons de la calculette.
 P( a  X  b ) :
2nde VARS
Exemple : P( 2  X  5 )  0,2544
2: normalFrep ( a,b,, )
si X suit une N( 6 , 2,4 )
 P( X  b ) = P( X  ] –  ; b ] ) : 2nde VARS
Exemple : P( X  5 )  0,2593
2: normalFrep ( –1*1099,b,, )
si X suit une N( 6 , 2,4 )
 P( X  a ) = P( X  [ a ; +  [ )
2nde VARS
Attention :  = 2,4
2: normalFrep ( a,1*1099,, )
Exemple : P( X  2 )  0, 99
51
si X suit une N( 6 , 2,4 )
Attention :  = 2,4
Attention :  = 2,4
Remarque : P( X  a ) = 1 – P( X  a )
Animation geogebra : visualisation_probas_normales.ggb
Parfois, dans certains exercices, on aura besoin de connaitre les valeurs de a ou de b pour qu'une
probabilité prenne une valeur fixée.
 Que vaut b pour que P( X  b ) =  ( réel connu compris entre 0 et 1 ) ?
2nde VARS 3: FracNormal ( ,, )
Attention, la calculette ne donne la réponse que pour ce type de probabilité.
Exemple : P( X  b )  0,95 si X suit une N( 6 , 2,4 ) Attention :  = 2,4
La calculette donne b  8,55
 Si on cherche a tel que P( X  a ) =  il faudra transformer l'écriture de la probabilité .
P( X  a ) =  devient 1 – P( X  a ) =  donc P(X  a ) = 1 – 
on tape alors 2nde VARS 3: FracNormal ( 1–,, ) et on obtient la valeur de a.
Exemple : P( X  a )  0,05 si X suit une N( 6 , 2,4 ) Attention :  = 2,4
P( X  a )  0,05 devient P(X  a ) = 1 – 0,05 = 0,95 La calculette donne a  8,55
 Si on cherche a tel que P( – a  X  a ) =  avec X une variable aléatoire centrée réduite
il faudra transformer l'écriture de la probabilité .
P( – a  X  a ) =  devient 2 P( 0  X  a ) =  car la courbe est symétrique par rapport à la droite
d'équation x = 0


 1 +1
d'où P(X  a ) – P ( X  0 ) = donc P(X  a ) = + =
2
2
2 2
2
+1
on tape alors 2nde VARS 3: FracNormal (
,0,1 ) et on obtient la valeur de a.
2
Exemple : P( –a  X  a )  0,6 si X suit une N( 0 , 1 ) .
P( –a  X  a )  0,6
0,6 + 1
devient P(X  a ) =
= 0,8.
2
La calculette donne a  0,84.
d'où P(0  X  a ) =
 Probabilités d'intervalles particuliers à connaitre :
Avec la loi normale N(  , ² ):
Avec la loi normale centrée réduite N( 0 , 1 ):
P (  –   X   +  )  0,68
P ( – 1  X  1 )  0,68
P (  – 2  X   + 2 )  0,95
P ( – 2  X  2 )  0,95
P (  – 3  X   + 3 )  0,997
P ( – 3  X  3 )  0,997
Démontrons que P (  –   X   +  )  0,68.
P(–X+)=P(–X–  )=P(–1
Si X suit une loi N(  , ² ) alors Z =
X–
 1)

X–
suit une loi N( 0 , 1 ).

x²
1
e – 2 dx .
2
X–
 1 ) = 1

–1
La calculette nous donne la valeur de cette intégrale : environ 0,68.
Donc P ( – 1 
P (  –   X   +  )  0,68
P (  – 2  X   + 2 )  0,95
P (  – 3  X   + 3 )  0,997
Animation geogebra : Un_deux_trois_sigma.ggb
4) Quelques exemples types :
Exemple 1 : On connait les paramètres de la loi normale et on fait des calculs de probabilité
avec la calculette.
La sélection chez les vaches de race FFPN " Française Frisonne à Pis Noir "
P( X  6250 )  0,27 ( calculette )
On cherche k tel que P(X  k ) = 0,3.
La calculette donne k  5790 L.
P(X  5800 )  0,31 ( calculette )
On cherche k tel que P(X  k ) = 0,2
donc P(X  k ) = 1 – 0,2 = 0,8 .
La calculette donne k  6337 L.
P( 5900  X  6100 )  0,20 ( calculette )
Exemple 2 : On connait la moyenne et on veut déterminer l'écart–type de manière à respecter une
règle de conformité.
X1 – 1,5
.
1
Y suit alors une loi normale centrée réduite de
moyenne 0 et d'écart–type 1.
P( 1,35  X  1,65 ) = 0,99
1,35 – 1,5
1,65 – 1,5
 P(
Y
) = 0,99
1
1
0,15
0,15
 P( –
Y 
) = 0,99
1
1
0,15
 2 P( 0  Y 
) = 0,99
1
0,15
0,99
 P( 0  Y 
)=
2
1
0,15
0,99
 P(Y 
)–P(Y0)=
2
1
0,15
0,99 1 1,99
 P(Y 
)=
+ =
2
2
2
1
0,15
La calculette nous donne
 2,576
1
d'où 1  0,06.
On pose Y =
P( 1,35  X  1,65 )  0,97.
Exemple 3 : On connait l'écart–type et on veut déterminer la moyenne de manière à respecter une
règle de conformité.
X –
.
2
Y suit alors une loi normale centrée réduite
de moyenne 0 et d'écart–type 1.
100 – 
P( X  100 ) = 0,001  P( Y 
) = 0,001
2
100 – 
La calculette nous donne
 – 3,09
2
d'où   106,18.
On pose Y =
Exemple 4 : On ne connait ni l'écart–type, ni la moyenne et on souhaite les déterminer de
manière à respecter une règle de conformité.
X –
.

Y suit alors une loi normale centrée réduite
de moyenne 0 et d'écart–type 1.
On pose Y =



 200–   1,036
 120 – 
   – 1,645
P( 120  X  200 ) = 0,8
P( X  120 ) = 0,05

 P( 120–   Y  200–  ) = 0,8

120 – 
 P(Y   ) = 0,05

 P( Y  200–  ) – P(Y  120–  ) = 0,8

120 – 
 P(Y   ) = 0,05

La calculette nous donne :
 P( Y  200–  ) = 0,8 + 0,05 = 0,85

120 – 
 P(Y   ) = 0,05

–
   200
1,036

200 – 
 120 –   – 1,645  1,036

   200 – 
1,036

 124,32 – 1,036   1,645  – 329

   200 – 
1,036

 2,681   453,32




  29,84
  169,09
III. Fluctuation et estimation :
1) Fluctuation d'échantillonnage :
Un échantillon statistique de taille n est la liste des résultats obtenus après n répétitions de la même
expérience aléatoire.
La distribution des fréquences associée à un échantillon est la liste des fréquences des issues de
l’échantillon.
Les distributions des fréquences varient d’un échantillon à l’autre pour une même expérience :
c’est ce qu’on appelle la fluctuation d’échantillonnage.
2) Intervalle de fluctuation asymptotique:
Si on note Fn la variable aléatoire qui, à tout échantillon de taille n, associe la fréquence d'un caractère.
Posons In l'intervalle
p(1–p)
; p + 1,96 
n
[ p – 1,96 
p(1–p)
n
]
avec p la proportion de ce caractère dans la population globale.
Alors Fn prend ses valeurs dans In avec une probabilité qui s'approche de 0,95 quand n devient grand.
Conditions pour mettre en pratique cette approximation :
n  30
;
np5
;
n(1–p)5
L'intervalle In est l'intervalle de fluctuation asymptotique au seuil de 95%.
3) Estimation d'une proportion inconnue à partir d'un échantillon :
On suppose maintenant que la proportion p du caractère dans la population globale n'est pas connue.
Notons f la fréquence observée dans un échantillon de taille n.
1
1
Alors l'intervalle f –
;f+
contient p avec une probabilité d'au moins 0,95.
n
n
Conditions pour mettre en pratique cette approximation :
[
n  30
;
]
nf 5
;
n(1–f )5
Cet intervalle est l'intervalle de confiance de p au niveau de confiance 0,95 ou au risque de 5 %.
4) Quelques exemples :
a) Intervalles de fluctuation :
19
= 0,19  I donc, il n'est pas necessaire
100
de lancer une investigation plus complète.
f =
13
87
;1–p=
et n = 100
100
100
Conditions : n = 100  30 ; np = 13  5 ;
n( 1– p) = 87  5
donc l'intervalle de fluctuation au seuil de 95%
sera:
p=
I = [0,13–1,96 
0,13  0,87
; 0,13+1,96 
100
0,13  0,87
]
100
Il faut trouver n tel que
0,13  0,87
0,13 + 1,96 
< 0,19
n
donc 1,96  0,13  0,87 < ( 0,19 – 0,13 ) n
1,96
donc n >
 0,13  0,87
0,06
donc n > 10,98 donc n > 120,7.
Il aurait suffit de prendre un échantillon d'au
moins 121 personnes pour devoir faire de
nouvelles études.
I = [ 0,064 ; 0,196 ]
b) Intervalles de confiance :
106
et n = 134.
134
Donc l'intervalle de confiance à 95%
106
1
106
1
sera J = [
–
;
+
]
134
134 134
134
J = [ 0,705;0,877]
f =
45
J = [ 0,492 ; 0,724]
74 u
52
Service hospitalier : n=60 ; f =
J = [ 0,738 ; 0,996]
60 h
Service d'urgence : n=74 ; f =
Les deux intervalles de confiance sont disjoints
donc on peut en déduire que les pratiques sont
différentes dans les deux services.