C10-TORSEURS

Chapitre X : Torseurs
Après une étude attentive de ce chapitre, vous serez capable
de :
• définir une application linéaire symétrique ou antisymétrique
• définir la matrice d’une application linéaire et de trouver ses
valeurs propres.
• effectuer les opérations de dérivation des vecteurs.
• énoncer les principales propriétés des torseurs
• montrer que le champ des vitesses d’un solide en mouvement est
un torseur

Mathématiques pour les Sciences Physiques
122
I Applications linéaires
1°- Définition
Soit f une application de E3 dans E3. f est linéaire si :
∀ u, v ∈ E3, f(u+v)=f(u)+f(v)
∀ λ ∈ R , ∀ u ∈ E3, f(λu)= λ f(u)
2°- Matrice d’une application linéaire
Soit (e1, e2, e3) une base orthonormée directe de E
3 et f une
application linéaire de E3 dans E3
Soit u ∈ E3 , on peut écrire : uei ==
∑ui
i1
3
D’après la linéarité de f on peut écrire :
f f u u f
i
ii i
( ) ( )ue e
i i
=
=
= =
∑ ∑
1
3
1
3
Ainsi, pour connaître l’application linéaire f, il suffit de connaître les
images par f de chacun des vecteurs de base.
En notant : faij
i
( )e e
ji
==
∑1
3, on peut écrire la relation précédente
sous forme matricielle pour obtenir la matrice colonne de f(u) sur la
base (e1, e2, e3):
[ ]
f
aaa
a a a
aaa
u
u
u
( )u=
11 12 13
21 22 23
13 23 33
1
2
3
ou
[
]
[
]
f( )uAu=
La matrice A associée à f est la matrice dont les colonnes sont les
coordonnées dans la base (e1, e2, e3) des images de e1, e2 et e3.

Torseurs
123
3°- vecteurs propres et valeurs propres
Un vecteur non nul u de E
3 est un vecteur propre de f si il
existe λ tel que :
f( )u
u
=
λ
λ est la valeur propre associée à u.
Pour trouver les valeurs propres d’une application linéaire, il suffit de
résoudre
f( )u
u
0
−
=
λ
avec u≠0, ce qui s’écrit matriciellement :
a a a
a a a
a a a
u
u
u
u
u
u
11 12 13
21 22 23
13 23 33
1
2
3
1
2
3
0
0
0
− =
λ
soit :
a a a
aaa
a a a
u
u
u
11 12 13
21 22 23
13 23 33
1
2
3
1 0 0
0 1 0
0 0 1
0
0
0
− =
λ
ceci ne pouvant être réalisé avec
(
)
(
)
u u u
1 2 3 0 0 0, , , ,≠ qu’en annulant
le déterminant de ce système, c’est à dire en annulant le polynôme
caractéristique de f :
det(
)
A
I
−
=
λ
0
4°- Applications symétriques et antisymétriques
Soit h une application de E3 dans E3.
h est symétrique si ∀ u, v ∈ E3 u⋅⋅h(v)=v⋅h(u)
h est antisymétrique si ∀ u, v ∈ E3 u⋅⋅h(v)=-v⋅h(u)
propriétés : une application symétrique ou antisymétrique est
nécessairement linéaire.

Mathématiques pour les Sciences Physiques
124
5°- Propriétés des applications linéaires symétriques
Soit hs une application symétrique (et donc linéaire) de E
3 dans
E3. Notons AS la matrice de hs dans une base orthonormée directe (e1,
e2, e3).
n AS=ASt où ASt est la matrice transposée de AS. Autrement dit, la
matrice de hs est symétrique : AS=
a q r
q a s
r s a
11
22
33
n Les valeurs propres de hs sont réelles.
n Il existe au moins une base orthonormée constituée de vecteurs
propres de hs. Dans cette base, la matrice de hs est diagonale :
λλλ
1
2
3
0 0
0 0
0 0
Remarque : quand on effectue la recherche des valeurs propres et des
vecteurs propres d’une application linéaire et que l’on exprime sa
matrice dans une base propre (c’est-à-dire une base constituée de
vecteurs propres), on dit que l’on diagonalise l’opérateur.
n enfin, si hs est une application linéaire symétrique définie positive,
c’est-à-dire si : ∀ u ∈ E3 , u⋅hs (u)>0
alors les valeurs propres de hs sont strictement positives.
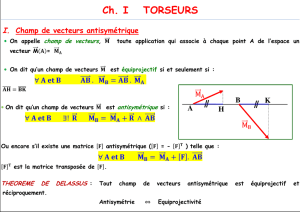
6°- Propriétés des applications linéaires antisymétriques
Soit ha une application antisymétrique (et donc linéaire) de E
3
dans E
3. Notons
[
]
AA=aij la matrice de ha dans une base
orthonormée directe (e1, e2, e3).
L’antisymétrie de ha conduit à : ∀ i, ei⋅ha(ei)=- ei⋅ha(ei), soit aij=0
∀ i,j , ej⋅ha(ei)=- ei⋅ha(ej), soit aij=-aji

Torseurs
125
La matrice de ha s’écrit donc : AA=−−
−
0
0
0
3 2
3 1
2 1
r r
r r
r r
et on peut
vérifier alors la propriété fondamentale :
[ ]
[ ] ∀ ∈ ==−−
−
= ×
u u Au
A
E,( )
3h
r r
r r
r r
u
u
u
r
r
r
u
u
u
a
0
0
0
3 2
3 1
2 1
1
2
3
1
2
3
1
2
3
On voit qu’il existe un unique vecteur R de E
3 appelé vecteur de
l’application linéaire antisymétrique qui permet d’écrire :
∀ ∈ = ×u u RuE,( )
3ha
7°- dérivation composée des vecteurs
En physique, pour décrire l’évolution spatio-temporelle des
objets étudiés (mobiles, champs, etc.) on utilise un repère spatial
matérialisé par des axes de coordonnées et
un repère temporel ou chronologie.
L’ensemble est appelé référentiel.
Ainsi, un événement se produisant
en M dans un référentiel R est repéré par
trois coordonnées spatiales (x1, x2, x3) et
une coordonnée temporelle t, soit un
quadruplet (x1, x2, x3, t)
Considérons deux référentiels
R et R’ en mouvement relatif et soit u
un vecteur fixe de R’, c’est à dire
dont les coordonnées (x1’, x2’, x3’) ne
dépendent pas de t. La dérivée de u
par rapport à R’ est nulle :
d
dt R
u0
=
'
x1
x3
x2
e3
e2 e1O
M
u
x3’
x2’
x1’
x1
x3
x2
e3
e2
e1O