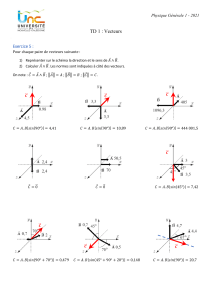
Exercice 2

1
Université M’HAMED BOUGARA BOUMERDES Année 2016-2017
Faculté des Sciences
Département de Physique
Physique 1 (ST)
Série N°1
(Analyse dimensionnelle)
Exercice 1 : Soit un pendule simple constitué d’une masse m accroché à un fil de masse
négligeable et de longueur l. On travaille dans le référentielle terrestre où le champ de
gravitation est .
Montrer par une analyse dimensionnelle, que la période T des petites oscillations de ce
pendule s’écrit sous la forme 
 .
Exercice 2 : Soit un gaz enfermé dans un récipient, la pression P qu’exerce ce gaz est due aux
chocs des molécules sur la paroi interne, à priori P dépend de la densité n du gaz (n est le
nombre des molécules par mètre cube ()), de la masse m de chaque molécule et de la
vitesse v moyenne de leur déplacement.
En utilisant l’analyse dimensionnelle, trouver la formule de la pression P à une constante
près.
(Calcul d’erreur)
Exercice 3 : Une masse m est lâchée d’une hauteur h, à son arrivée au sol, elle avait une
vitesse  . Si la hauteur h = 53.6m, mesurée avec une erreur de 1cm, l’accélération
gravitationnelle, g=9.81m/s2, est connue avec une précision de 0.1%, estimer l’erreur sur la
valeur de la vitesse v calculée.
Dans tout ce qui suit, on considère un repère orthonormé de vecteurs unitaires .
(Calcul vectoriel)
Exercice 4 : Soient les vecteurs 
 -2  +
, 
 -4  -3
, 
 +2  +2
1) Trouver les modules de : 
 ,   , 
2) Trouver les angles (

2
Exercice 5 : Evaluer chacun des vecteurs suivants : 
, 
,  ,  ,  , 
,  .
Exercice 6 : Reprendre les vecteurs de l’exercice 3, trouver le résultat s’il existe, en précisant
la nature (scalaire ou vecteur) :
,  ,  , 
Exercice 7 : Soient les vecteurs   + ,  +
Calculer : 
 ,   , puis le module de chacun de ces vecteurs.
Exercice 8: Une force   provoque le mouvement d’un corps qui se
déplace suivant le vecteur déplacement :  + (m).
1) Trouver W= (le travail de la force F)
2) Déduire la projection de la force 
 sur le vecteur déplacement 
.
3) Trouver la relation entre les composantes du vecteur déplacement  et
, pour que le travail de 
 soit nul.
Exercice 9 : Soit 
 -2
et  + (2X2-X)
1) Calculer 
 et 
dans le cas où X=0 et X=1
2) Calculer   de deux manières différentes
Soit G(X,Y,Z)=3X2+9XY-6Y2Z-3XZ+5XYZ2 une fonction dans l’espace cartésien.
3) Calculer 
Soit 
=(x2+1)
4) Calculer 
.