Tableau 1

1
Analyse des données:
Pièces de 1 cent:
données des années
précédentes

2
Tableau 1
Données brutes - tableau partiel,
> 1500 pièces
1 p0779316 1976 t.o 19.0 1.5 3.2102
2 p0779316 1979 t.o 19.0 1.5 3.2542
3 p0779316 1981 t.o 19.0 1.5 2.7052
4 p0779316 1994 l.o 19.0 1.5 2.5004
5 p0779316 1997 n 19.0 1.5 2.2375
6 p0779316 1999 o 19.0 1.5 2.2366
7 p0779316 2001 l.o 19.0 1.5 2.2476
8 p0779316 2004 n 19.0 1.5 2.2481
9 p0779316 2005 l.o 19.0 1.5 2.2207
10 p0779316 2006 n 19.0 1.5 2.2243
11 p0820214 1976 o. 19.0 1.5 3.3042
12 p0820214 1978 t.o. 19.0 1.5 3.2810
13 p0820214 1983 t.o. 19.0 1.5 2.4839
14 p0820214 1986 o. 19.0 1.5 2.4899
15 p0820214 1989 t.o. 19.0 1.5 2.5128
16 p0820214 1999 l.o. 19.0 1.5 2.2608
17 p0820214 2001 n. 19.0 1.5 2.2564
18 p0820214 2003 l.o. 19.0 1.5 2.3817
19 p0820214 2005 n. 19.0 1.5 2.2426
20 p0820214 2006 n. 19.0 1.5 2.2691
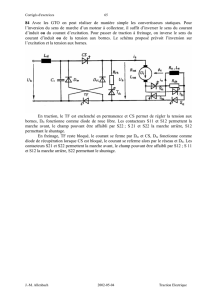
Tableau 1.
Étude portant sur les masses de pièces de monnaie canadienne de 1 cent.
TP1, module 2
Compteur
Code de
l'étudiant
Année de
frappe
État de la
pièce
diamètre/
mm
épaisseur
/mm
masse/g

3
Analyse des résultats
•Trois objectifs:
– Établissement du nombre de chiffres significatifs d’une
valeur et intervalle de confiance
–Comparaison des résultats
–Choix du meilleur modèle mathématique pour représenter un
ensemble de données expérimentales: moyenne, droite (m
et b), autre modèle…

4
Analyse tableau 1: Moyenne
•Avec Excel
–Utilitaire d’analyse:
sous l’onglet «Outils»
• Si l’utilitaire n’est pas
présent, ouvrir «macros
complémentaires» et cocher
l’outil « utilitaire d’analyse ».
–Choisir «Statistiques
descriptives»
•Trouver la masse moyenne
des valeurs du tableau qui se
trouvent dans la colonne G,
de G8 à G1528 (1521
valeurs)

5
Résultats pour la masse
1.9600.3646
1521
= s= s2