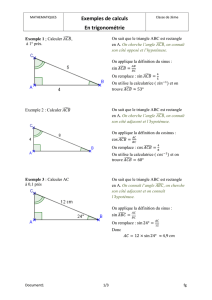
1 Vocabulaire et notations 2 Relations trigonométriques dans le

Collège Elie COUTAREL
Année 2009-2010.
G.MANDALLAZ.
Ecrit avec L
A
T
EX
Trigonométrie dans le triangle
rectangle
1 Vocabulaire et notations
On considère un triangle ABC rectangle en B.
Lorsqu’il n’y a pas de confusion possible, on note respectivement b A, b Bet b Cles angles
\
BAC,
\
ABC et
\
ACB.
Le côté [AC]du triangle est particulier, on dit qu’il est l’hypoténuse du triangle.
Relativement à l’angle b A:
i[BC]est le côté opposé (le côté "en face" de l’angle).
i[AB]est le côté adjacent (le côté qui touche l’angle et qui n’est pas l’hypoténuse).
Relativement à l’angle b C:
i. . . . . . est le côté opposé.
i. . . . . . est le côté adjacent.
2 Relations trigonométriques dans le triangle rectangle
Dans cette partie, on considère un triangle ABC rectangle en B.
2.1 Cosinus d’un angle aigu
Définition 1
On appelle cosinus de l’angle ˆ Ale rapport : cos b A=Côté adjacent de b
A
Hypoténuse .
cos ˆa=AB
AC
Exercice 1
Exprimer cos b C.
1

2.2 Sinus d’un angle aigu
Définition 2
On appelle sinus de l’angle ˆ Ale rapport : sin b A=Côté opposé de b
A
Hypoténuse .
sin ˆ A=BC
AC
Exercice 2
Exprimer sin b C.
2.3 Tangente d’un angle aigu
Définition 3
On appelle tangente de l’angle ˆ Ale rapport : tan b A=Côté opposé de b
A
Côté adjacent de b A.
tan ˆ A=BC
AB
Exercice 3
Exprimer tan b C.
2.4 Procédé mnémotechnique et valeurs remarquables
Pour se rappeler des formules, on peut utiliser le procédé mnémotechnique suivant qui devrait plaire à la plupart
d’entre vous : CAHSOHTOA
En lisant ce "mot", il est facile de se le rappeler en faisant attention à la place des H.
CAH : Cosinus=Adjacent/Hypoténuse.
SOH : Sinus=Opposé/Hypoténuse.
TOA : Tangente=Opposé/Adjacent.
Les valeurs trigonométriques sont rarement des nombres décimaux, pourtant il est conseillé de connaître cer-
taines valeurs par coeur :
Angle α(en ◦) 30 45 60
cos α√3
2
√2
2
1
2
sin α1
2
√2
2
√3
2
tan α√3
31√3
Remarque 1
Vous verrez l’année prochaine une extension des lignes trigonométriques à n’importe quel nombre réel.
2

2.5 Exemples
Exemple 1
On considère un triangle T RI rectangle en T. Sachant que
[
T RI = 30◦et RI = 5, calculer T I.
Indic : Sur le brouillon faites apparaître ce que représentent le côté dont la mesure est donnée ainsi que le côté
cherché (relativement à l’angle donné).
Exemple 2
On considère un triangle GON rectangle en G. Sachant que
\
GON = 60◦et OG = 2, calculer ON.
Exemple 3
On considère un triangle OME rectangle en O. Sachant que
\
OME = 45◦et OE = 7, calculer OM.
Exemple 4
On considère un triangle T RI rectangle en T. Sachant que T R = 4 et RI = 6, calculer
[
T RI.
Indic : Sur le brouillon faites apparaître ce que représentent les deux côtés dont on connaît la mesure (relati-
vement à l’angle que l’on cherche).
Exemple 5
On considère un triangle EIL rectangle en E. Sachant que EL = 3 et EI = 2, calculer
[
EIL.
Exemple 6
On considère un triangle OV E rectangle en O. Sachant OE = 3 et V E = 7, calculer
\
OV E.
3 Propriétés des fonctions trigonométriques
Propriété 1
Si ˆ Aest un angle aigu alors :
l0<cos ˆ A < 1.
l0<sin ˆ A < 1.
l0<tan ˆ A.
Démonstration 1
Cet angle correspond à un triangle ABC rectangle en B.
Ainsi cos b A=AB
AC ;sin b
A=BC
AC et tan b
A=BC
AB .
Comme quotient de longueurs on a déjà 0<cos b A;0<sin b Aet 0<tan b A.
Comme ABC est rectangle en B, on a AB < AC et BC < AC (AC est l’hypoténuse).
Donc cos b A < 1et sin b A < 1.¥
3

Propriété 2
Si ˆ Aest un angle aigu alors : tan ˆ A=sin ˆ
A
cos ˆ Aet cos2ˆ
A+ sin2ˆ A= 1.
Démonstration 2
Cet angle correspond à un triangle ABC rectangle en B.
Ainsi tan b A=BC
AB et sin b
A
cos b A=
BC
AC
AB
AC
=BC
AC ×AC AB =BC AB .
Donc tan b A=sin b
A
cos b A.
cos2b A+ sin2b A=µAB
AC ¶2
+µBC
AC ¶2
=AB2+BC2
AC2=AC2 AC2= 1 (d’après le théorème de Pythagore).¥
4