Correction du devoir 10 classe de 5 e

Correction du devoir 10 classe de 5 e
Pour les parents qui aident leur enfants. Le but à atteindre dans ce devoir est de
montrer que la médiane dans un triangle partage le triangle en deux triangles de même aire.
Les enfants ne doivent donc pas utiliser cette propriété et ils n'ont pas pas besoin de connaître
la définition de la médiane. Le bilan est fait en classe afin de montrer aux élèves le fil
conducteur de l'exercice.
Pour atteindre ce but, les élèves doivent utiliser uniquement les propriétés de la symétrie
centrale . Ce devoir leur permet donc de réinvestir tout ce qui a été vu sur cette symétrie et dans ce
corrigé j'ai mis en rouge toutes les propriétés que les élèves ont à leur disposition pour mener à bien
ce travail. Ce corrigé va leur permettre de revoir les propriétés essentielles de géomètrie auxquelles
il faudra ajouter les proprietés sur les parallélogrammes particuliers.
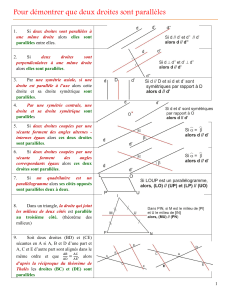
Données: RCO est un triangle
RC = 7 cm, RO = 6 cm et CO = 10 cm
I le milieu de [CO]
T le milieu de [RC]
A le symétrique du point I par rapport au point T
J milieu de [RO]
V est le symétrique du point I par rapport au point J
4) Que puis-je dire des droites (AC) et (VO) ?
Ma démarche: Sur le dessin , je vois que les droites sont parallèles.
Rappel de cours: que puis-je utiliser pour montrer que des droites sont parallèles?
Ma boîte à outils: J'ai à ma disposition les théorèmes suivants:
Propriété 1: Si deux droites sont perpendiculaires à la même droite alors elles sont parallèles
Propriété 2: Si deux droites sont parallèles à la même droite alors elles sont parallèles
Propriété 3: Si un quadrilatère est un parallélogramme, alors ses côtés opposés sont parallèles.

Propriété 4: Si une droite est parallèle à l'axe dans une symétrie axiale alors la droite symétrique
est parallèle à l'axe.
Propriété 5: Si deux droites sont symétriques dans une symétrie centrale alors elles sont parallèles.
Propriété 6: Si deux angles alternes-internes ou deux angles correspondants sont égaux alors ils
sont déterminés par deux droites parallèles et une sécante
Que puis-je utiliser?
Dans le texte on m'a fait tracer des symétriques de triangles par rapport à un point, donc je
vais utiliser le théorème 5 et le théorème 2.
Ma démonstration:
Etape 1: je montre que :les droites (AC) et (RI) sont parallèles.
Données Propriété Conclusion
Etape 1: Par la symétrie de
centre T, l'image du point A est
le point I et l'image du point C
est le point R , l'image de la
droite (AC) est la droite (RI)
Si deux droites sont
symétriques par rapport à un
point alors elles sont parallèles
Donc les droites (AC) et (RI)
sont parallèles.
Etape 2: je montre que :les droites (AC) et (RI) sont parallèles.
Données Propriété Conclusion
Etape 2: : Par la symétrie de
centre J, l'image du point R est
le point O et l'image du point I
est le point V , l'image de la
droite (RI) est la droite (VO)
Si deux droites sont
symétriques par rapport à un
point alors elles sont parallèles
Donc les droites (VO) et (RI)
sont parallèles.
Etape 3: je montre que :les droites (AC) et (VO) sont parallèles.
Données Propriété Conclusion
Etape 3: les droites (AC) et (RI)
sont parallèles
et les droites (VO) et (RI) sont
parallèles.
Si deux droites sont parallèles à
une même droite alors elles sont
parallèles.
Les droites (AC) et (VO) sont
parallèles.
5) Je montre que le point R est le milieu du segment [AV].
Ma boîte à outil: comment montrer qu'un point est le milieu d'un segment
Propriété 1: Si un point est sur un segment et à égale distance de ses extrémités du segment alors
ce point est au milieu du segment
Propriété 2: Si une droite est la médiatrice d'un segment alors elle coupe le segment en son milieu.
Propriété 3: Si un point est la milieu d'un segment alors le symétrique de ce point est le milieu du
segment symétrique.

Propriété 4: Si un point est situé sur un segment et qu'il est à égale distance des extrémités du
segment alors c'est le milieu du segment
Propriété 5: si un quadrilatère est un parallélogramme alors ses diagonales se coupent en leur
milieu
Ici pour montrer que le point est le milieu d'un segment, je dois montrer que le point est sur
le segment et à égale distance des deux extrémités du segment
Démarche:
Pour prouver que R est milieu de [AV], je dois montrer que les points A, R et V sont alignés.
et que AR = RV.
Pour prouver que les points sont alignés, je vais montrer que les droites (AR) et (RV) sont
parallèles et commes ces droites ont un point commun alors elles seront confondues.
Rappel de cours: que puis-je utiliser pour montrer que des droites sont parallèles?
Ma boîte à outils: J'ai à ma disposition les théorèmes suivants:
Propriété 1: Si deux droites sont perpendiculaires à la même droite alors elles sont parallèles
Propriété 2: Si deux droites sont parallèles à la même droite alors elles sont parallèles
Propriété 3: Si un quadrilatère est un parallélogramme, alors ses côtés opposés sont parallèles et
égaux..
Propriété 4: Si une droite est parallèle à l'axe dans une symétrie axiale alors la droite symétrique
est parallèle à l'axe.
Propriété 5: Si deux segments sont symétriques par rapport à un point ils sont parallèles et égaux
Propriété 6: Si deux angles alternes-internes ou deux angles correspondants sont égaux alors ils
sont déterminés par deux droites parallèles et une sécante
Que puis-je utiliser?
Dans le texte on m'a fait tracer des symétriques de triangles par rapport à un point, donc je
vais utiliser la propriété 5

Je montre que le point R est le milieu de [AV]
Méthode 1: en utilisant la symétrie centrale
Je prouve d'abord que les points A, R et V sont alignés
Etape 1 : je montre que les droite (AR) et (CI) sont parallèles
Données Propriété Conclusion
Etape 1: Par la symétrie de
centre T, l'image du point A est
le point I et l'image du point C
est le point R , l'image de la
droite (AR) est la droite (CI)
Si deux droites sont
symétriques par rapport à un
point alors elles sont parallèles
Donc les droites (AR) et (CI)
sont parallèles
Etape 2: Je montre que les droites (RI) et (VO)sont parallèles
Données Propriété Conclusion
Etape 2: Par la symétrie de
centre J, l'image du point R est
le point O et l'image du point I
est le point V , l'image de la
droite (RI) est la droite (VO)
Si deux droites sont
symétriques par rapport à un
point alors elles sont parallèles
Donc les droites (RI) et
(VO)sont parallèles
Etape 3: Je montre que les points A, R et V sont alignés
Données Propriété Conclusion
Etape 3: les droites (AR) et)
(CI) sont parallèles
et les droites (RI) et (VO)sont
parallèles
Si deux droites sont parallèles à
une même droite alors elles sont
parallèles.
Donc les droites (AR) et (RV)
sont parallèles comme elles ont
un point commun alors elles
sont confondues donc les points
A, R et V sont alignés
Je vais montrer que : AR = RV
Données Propriété Conclusion
Par la symétrie de centre T
l'image du segment [AR] est le
segment [CI]
et par la symétrie de centre J
l'image du segment [VR] est le
segment [IO]
CI = IO
Si deux segments sont
symétriques alors ils ont la
même mesure
Donc AR = CI et VR = IO et
comme CI =IO
alors AR = VR
Les points A, R et V sont alignés dans cet ordre et AR = VR donc R est le milieu du segment
[AV]

Méthode 2 en utilisant le théorème 2 mais au préalable il faut prouver que les quadrilatères
ARIC et RVOI sont des parallélogrammes.
Ma boîte à outil pour prouver qu'un quadrilatère est un parallélogramme
Propriété 1: Si un quadrilatère a des diagonales qui se coupent en leur milieu alors c'est un
parallélogramme
Propriété 2: si un quadrilatère non croisé a un centre de symétrie alors c'est un parallélogramme
Propriété 3: si un quadrilatère a ses côtés parallèles deux à deux alors c'est un parallélogramme
Pour prouver que ARIC et RVOI sont des parallélogrammes, je vais utiliser la proporiété 2
Je montre que les quadrilatères ARIC et RVOI sont des parallélogrammes
Données Propriété Conclusion
Par la symétrie de centre T
l'image du point A est le point I
et l'image du point C est le
point R
et par la symétrie de centre J
l'image du point V est le point I
et l'image du point O est le
point R
Si un quadrilatère non croisé a
un centre de symétrie alors c'est
un parallélogramme
Les quadrilatères ARIC et
RVOI sont des
parallélogrammes
Je montre que les points A, R et V sont alignés
Données Propriété Conclusion
Les quadrilatères ARIC et
RVOI sont des
parallélogrammes
Si un quadrilatère est un
parallélogramme alors ses côtés
opposés sont parallèles
Donc les droites ( AR) et (CI)
d'une part et les droites ( VR) et
(IO) sont parallèles et comme
les points I, O et C sont alignés
alors les droites (AR) et (RV)
sont parallèles et elles passent
par le point R donc elles sont
confondues et les points A, R et
V sont alignés