Opérations sur les nombres décimaux (2)

Cours 6ème 1
Opérations sur les nombres décimaux (2)
1. Division euclidienne
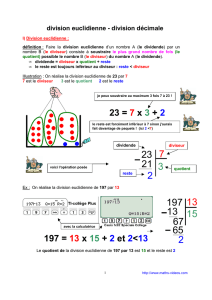
Définition : Effectuer la division euclidienne d’un entier (le dividende) par un autre entier différent de
zéro (le diviseur), c’est trouver deux autres nombres entiers, le quotient et le reste, tels que
dividende = (diviseur x quotient) + reste avec reste < diviseur.
Exemple : dividende diviseur
329 8
-32 41
09 quotient
- 8
reste 1
Ainsi : 329 = 8 x 41 + 1 ou 329 = 41 x 8 + 1.
Remarque : Pour effectuer cette division euclidienne, on se demande : « Dans 329, combien de fois 8 ? ».
Ainsi : « Dans 329, il y a 41 fois 8 et il reste 1. ».
2. Critères de divisibilité
Critères de divisibilité par 2, 5 ou 10 : Un nombre entier est multiple de :
 2 si son chiffre des unités est 0 ; 2 ; 4 ; 6 ou 8. On dit que c’est un nombre pair.
 5 si son chiffre des unités est 0 ou 5.
 10 si son chiffre des unités est 0.
Exemples :
 184 est multiple de 2 car son chiffre des unités est 4.
 765 est multiple de 5 car son chiffre des unités est 5.
 340 est multiple de 2, de 5 et de 10 car son chiffre des unités est 0.
Critères de divisibilité par 3, 4 ou 9 : Un nombre entier est multiple de :
 3 lorsque la somme de ses « chiffres » est multiple de 3.
 9 lorsque la somme de ses « chiffres » est multiple de 9.
 4 lorsque le nombre formé par ses deux derniers chiffres est multiple de 4.
Exemples :
 501 est multiple de 3 car 5 + 0 + 1 = 6 et 6 est multiple de 3 (6 = 3 x 2).
 954 est multiple de 9 car 9 + 5 + 4 = 18 et 18 est multiple de 9 (18 = 9 x 2).
 732 est multiple de 4 car 32 est multiple de 4 (32 = 4 x 8).

Cours 6ème 2
3. Division décimale.
Définition : Effectuer la division décimale d’un nombre décimal (le dividende) par un nombre entier
différent de zéro (le diviseur), c’est trouver un autre nombre, le quotient, tel que
dividende = diviseur x quotient.
Exemple :
16,1 7
- 14
2,3
21
- 21
0
Ainsi : 16,1 = 7 x 2,3 ou 16,1 = 2,3 x 7.
Vocabulaire :
11 3
- 9
3,66
20
- 18
20
- 18
2
Si on poursuit l’opération, la division ne s’arrête jamais donc le quotient de 11 par 3 n’est pas un nombre
décimal.
On dit que 11 ÷ 3, que l’on écrit aussi 11
3 est la valeur exacte du quotient de 11 par 3.
On dit que 3,66 est une valeur approchée au centième par défaut de ce quotient.
Propriétés :
 Pour diviser un nombre par 10, on déplace la virgule d’un rang vers la gauche.
 Pour diviser un nombre par 100, on déplace la virgule de deux rangs vers la gauche.
 Pour diviser un nombre par 1 000, on déplace la virgule de trois rangs vers la gauche.
Remarque : Diviser un nombre par 10, 100 ou 1 000 revient à multiplier ce nombre respectivement par
0,1 ; 0,01 ou 0,001.