8.Trigonométrie dans le triangle rectangle 1) Définitions

8.Trigonométrie dans le triangle rectangle
1) Définitions
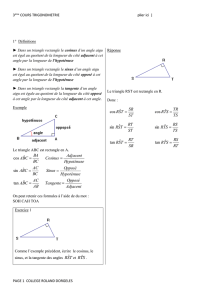
Dans un triangle rectangle, on a :
Cosinus d'un angle aigu =
longueur du côté adjacent à cet angle
longueur de l ' hypoténuse
Sinus d'un angle aigu =
longueur du côté opposé à cet angle
longueur de l ' hypoténuse
Tangente d'un angle aigu =
longueur du côté opposé à cet angle
longueur du côté adjacent à cet angle
Remarque :
En pratique, la formule « CAHSOHTOA » permet de retenir les définitions
du cosinus, du sinus et de la tangente d'un angle aigu d'un triangle
rectangle.
Exemple :

2) Utilisation de la calculatrice
La touche Cos de la calculatrice permet de calculer le cosinus d'un angle
aigu donné.
Inversement, si l'on connaît le cosinus d'un angle, on peut retrouver une
valeur approchée de cet angle à l'aide de la touche Arccos ou
cos−1
.
On utilisera, de même, les touches Arcsin ou
sin−1
pour le sinus et
Arctan ou
tan−1
pour la tangente.
Exemples :
(vous donnerez les valeurs exactes lorsque c’est possible, sinon, arrondir
au centième).
Quel est le sinus d’un angle de 34° ?
Quelle est la mesure d’un angle dont le cosinus vaut 0,3 ?
Quelle est la tangente d’un angle de 13° ?
3) Applications
Exemple 1 : Calculer une longueur
On considère un triangle LEO rectangle en E tel que :
LO = 5,4 cm et
^
ELO
= 62°.
a) Calcule la longueur du côté [OE] arrondie au millimètre.
b) Calcule ensuite la longueur du côté [EL] arrondie au millimètre.
62°
5,4 cm
O
L
E

a) Dans le triangle LEO rectangle en E,
Sin
^
ELO
=
côté opposé à
^
ELO
hypoténuse
Sin
^
ELO
=
OE
LO
Sin 62°=
OE
5,4
OE = 5,4 × sin 62°
OE ≈ 4,8 cm
La valeur approchée de OE arrondie au mm est 4,8 cm.
b) Dans le triangle LEO rectangle en E,
cos
^
ELO
=
côté adjacent à
^
ELO
hypoténuse
cos
^
ELO
=
EL
LO
cos 62°=
EL
5,4
EL = 5,4 × cos 62°
EL ≈ 2,5 cm.
La valeur approchée de EL arrondie au mm est 2,5 cm.

Exemple 2 : Calculer un angle
Soit FUN un triangle rectangle en U tel que :
UN = 8,2 cm et UF = 5,5 cm.
Calcule la mesure de l'angle
^
UNF
arrondie au degré.
Dans le triangle FUN rectangle en U,
tan
^
UNF
=
côté opposé à
^
UNF
côté adjacent à
^
UNF
tan
^
UNF
=
UF
UN
tan
̂
UNF
=
5,5
8,2
̂
UNF
=
tan−1(5,5
8,2 )
̂
UNF
≈ 34°.
F
U
8,2 cm
N
5,5 cm