Modèle mathématique. Ne pas hésiter à consulter

Toutes ces fiches sont téléchargeables gratuitement sur www.asblentraide.be – cos, sinus et tangente dans un triangle rectangle - Page 1
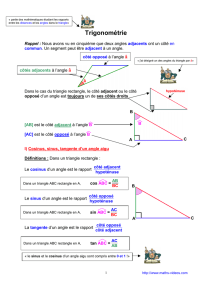
Maintenant que tu maîtrises les notions de côtés adjacents et côtés opposés, nous allons
pouvoir définir le cosinus d’un angle aigu ainsi que ses compagnons : le sinus et la tangente.
Reprenons notre triangle rectangle en B.
Ainsi donc
cos  = longueur du côté adjacent
longueur de l’hypoténuse = longueur du côté AB longueur du côté AC
Ainsi donc
sin  = longueur du côté opposé
longueur de l’hypoténuse = longueur du côté BC longueur du côté AC
côté opposé à l’angle C
COSINUS, SINUS ET TANGENTE DANS UN TRIANGLE RECTANGLE
Mise à jour : 01/02/13
Le cosinus de l’angle  est simplement un rapport de deux longueurs :
celle du côté adjacent à l’angle  et celle de l’hypoténuse.
Le sinus de l’angle  est un autre rapport de deux longueurs :
celle du côté opposé à l’angle  et celle de l’hypoténuse.

Toutes ces fiches sont téléchargeables gratuitement sur www.asblentraide.be – cos, sinus et tangente dans un triangle rectangle - Page 2
Ainsi donc
tan  = longueur du côté opposé
longueur du côté adjacent = longueur du côté BC longueur du côté AB
Un autre exemple ?
cos F = longueur du côté FK
longueur du côté FG cos G = longueur du côté GK longueur du côté FG
sin F = longueur du côté GK
longueur du côté FG sin G = longueur du côté FK longueur du côté FG
tan F = longueur du côté GK
longueur du côté FK tan G = longueur du côté FK longueur du côté GK
La tangente de l’angle  est encore un troisième rapport de deux longueurs :
celle du côté opposé à l’angle  et celle du côté adjacent.