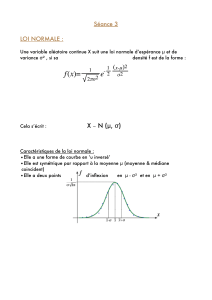
Variables aléatoires discrètes

X X(Ω)
x∈RA⊂R
[X=x] = X−1(x) = {ω∈Ω; X(ω) = x}
[X∈A] = X−1(A) = {ω∈Ω; X(ω)∈A}
([X=x])x∈X(Ω)
©
GXΩ = J1,6K2X(Ω) =
J2,12K
GX
Ω = {P, F P, F F P, . . .}∪{F F F F F . . .}
| {z }
ω0
X ω =ω0
P(ω0)=0 X X(Ω) =
N
X Y Ω
α
X+αY XY
X
X
PX:X(Ω) →R+
x7→ P([X=x])

©
X
Ω = J1,6K2X(Ω) = J2,12K
X
©X
X
XN
∀k≥1,P(X=k) = P([X≤k]) −P([X≤k−1])
X F
F X
X
XX
x∈X(Ω)
xP([X=x])
XE(X)
E(X) = X
x∈X(Ω)
xP([X=x])
N
XN
XX
k≥0
kP([X=k])
E(X) =
+∞
X
k=0
kP([X=k])
©X
X

©
X
X
X
φ:R→RX(Ω)
φ◦X: Ω →R
ω7→ φ(X(ω))
φ◦X φ(X)
X
φ:R→RX(Ω)
φ(X)X
x∈Ω(X)
φ(x)P([X=x])
E(φ(X))
E(φ(X)) = X
x∈Ω(X)
φ(x)P([X=x])

n
XJ1, nKX(Ω) = J1, nK
∀k∈J1, nK,P([X=k]) = 1
n
X → U(J1, nK)
a, b a < b
XJa, bKX(Ω) = Ja, bK
∀k∈Ja, bK,P([X=k]) = 1
b−a+ 1
X → U(Ja, bK)
©
GX
J1,6K
Gn1n
XJ1, nK
XJa, bK
X
E(X) = a+b
2,V(X) = (b−a)(b−a+ 2) 12
XJ1, nK
X
E(X) = n+ 1
2,V(X) = n2−1 12
∗

p∈]0,1[
X p X(Ω) = {0,1}
P([X= 1]) = p, P([X= 0]) = 1 −p
X → B(p)
©
G1
2
G
1 0
GX p X2
GX Y XY XY = 0
X p
X
E(X) = p, V(X) = p(1 −p)
∗