Chap.04 1− Cosinus, sinus, tangente a. Définition Dans un triangle

− Troisième −
− Chap.04 − http://jacobinsmaths.free.fr
1
Chap.04 T RIGONOMETRIE
1− Cosinus, sinus, tangente
a. Définition
Dans un triangle rectangle,
le Cosinus d’un angle aigu est égal au quotient côté Adjacent
Hypoténuse ;
le Sinus d’un angle aigu est égal au quotient côté Opposé
Hypoténuse ;
la Tangente d’un angle aigu est égal au quotient côté Opposé
côté Adjacent.
Voici un moyen mnémotechnique pour retenir les formules : CAH SOH TOA = « casse-toi »
Dans un triangle ABC rectangle en A,
BC est l’hypoténuse ;
AB (ou BA) est le côté adjacent à l’angle a ABC ;
AC (ou CA) est le côté opposé à l’angle a ABC.
On a donc les relations trigonométriques suivantes :
cos ABC = BA
BC sin ABC = AC BC tan ABC = AC AB
b. Propriété
Exemples :
Angles aigus 10° 30° 45° 60° 80°
Cosinus 0,985… 0,866… 0,707… 0,5 0,174…
Sinus 0,174… 0,5 0,707… 0,866… 0,985…
Tangente 0,176… 0,577… 1 1,732… 5,671…
Le cosinus et le sinus d’un angle aigu sont des nombres compris entre 0 et 1.
La tangente d’un angle est un nombre positif qui peut être plus grand que 1.
A
C
B
P
Côté opposé
à l’angle d P
Hypoténuse
Côté adjacent
à l’angle d P

− Troisième −
− Chap.04 − http://jacobinsmaths.free.fr
2
c. Exemples
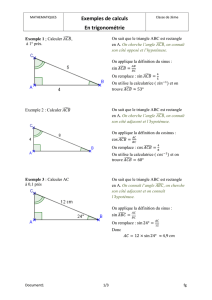
Enoncé 1 ABC est un triangle rectangle en C.
Donner la valeur exacte de BC, puis son arrondi à 1 mm près.
Solution
Dans le triangle ABC rectangle en C, on a :
tan a CAB = BC
AC
Remarque : tan 30° ≈ 0,577
tan 30°
1 = BC
4
On remplace et on rajoute 1 en dénominateur.
BC = 4 x tan 30° Produit en croix
La valeur exacte de BC est (4xtan30°) cm.
BC ≃ 2,3 La valeur approchée de BC à 1 mm près est 2,3 cm (ou 23 mm).
Enoncé 2 ABC est un triangle rectangle en A.
Donner la valeur exacte de BC, puis son arrondi à 1 mm près.
Solution
Dans le triangle ABC rectangle en A, on a :
cos a ABC = AB
BC
Remarque : cos 40° ≈ 0,766
cos 40°
1 = 5
BC
On remplace et on rajoute 1 en dénominateur.
BC = 5
cos 40°
Produit en croix
La valeur exacte de BC est 5
cos 40 cm.
BC ≃ 6,5 cm La valeur approchée de BC à 1 mm près est 6,5 cm (ou 65 mm).
Enoncé 3 ABC est un triangle rectangle en B tel que : AC = 2 cm et BC = 1,3 cm.
Déterminer la mesure de l’angle BAC au degré près.
Solution
Dans le triangle ABC rectangle en B, on a :
sin a BAC = BC
AC
sin a BAC = 1,3
2
donc a BAC ≃ 40,5
La mesure de l’angle a BAC au degré près est 41°.
0,
577
0,
577
0,
766
0,
766
B
C
A
40°
5
Je connais le côté
adjacent à
a
ABC
Je cherche
l’hypoténuse
C
A
B
30°
4 cm
Je connais le côté
adjacent à a CAB
Je cherche le côté
opposé à a CAB
C
A
B
1,3
2
Je connais
l’hypoténuse
Je connais le côté
opposé à
a
BAC
?

− Troisième −
− Chap.04 − http://jacobinsmaths.free.fr
3
2− Formules liant le cosinus, le sinus et la tangente
Dans un triangle rectangle, en considérant x la mesure de l’un des angles aigus, on a :
Démonstration :
Dans le triangle ABC rectangle en B,
x désigne l’angle aigu a BAC
(cos x )
2
+ (sin x )
2
= AB
AC
2
+ BC
AC
2
sin
x
cos x
=
BC
AC
AB
AC
= BC
AC x AC AB
= AB
2
AC
2
+ BC
2
AC
2
= BC x AC
AC x AB
= AB
2
+ BC
2
AC
2
= BC
AB
= 1 = tan x
Car le triangle ABC est rectangle en B
D’après le théorème de Pythagore on a :
AB
2
+ BC
2
= AC
2
E XERCICE TYPE
Enoncé :
Calcule la valeur exacte de sin d A et tan d A sachant que d A est un angle aigu et cos d A = 0,8.
Solution :
On sait que (cos d A )
2
+ (sin d A )
2
= 1
(0,8)
2
+ (sin d A )
2
= 1
0,64 + (sin d A )
2
=1
(sin d A )
2
= 1 – 0,64 = 0,36
sin d A = 0,36 donc sin d A = 0,6
On sait aussi que tan d A = sin d
A
cos d A
= 0,6
0,8 donc tan d
A = 0,75
(cos
x
)² + (sin
x
)² = 1
tan x =
sin
x
cos x
pour x ≠ 0°
B
A
C
x