Cours de mathématiques 3eannée niveau 2 Analyse 2012 – 2013

Cours de mathématiques
3eannée niveau 2
Analyse
2012 – 2013
Bernard Lenggenhager : b[email protected]h
Collège de Genève
Version du 5 janvier 2013

ii

Table des matières
Table des matières iii
1 Introduction 1
2 Entrée en matière 3
3 Principes de base 5
4 Limite 11
4.1 Notion de limite ................................. 11
4.2 Propriétés des limites .............................. 12
4.3 Asymptotes ................................... 14
5 Continuité 19
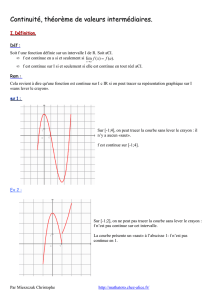
5.1 Continuité en un point ............................. 19
5.2 Continuité sur I................................. 21
6 Dérivée 25
6.1 La dérivée .................................... 25
6.2 Règles de dérivation .............................. 27
7 Calcul diff. 31
7.1 Les accroissements finis ............................. 31
7.2 Croissance .................................... 33
7.3 Extremum relatif ................................ 34
7.4 Courbure .................................... 35
8 Étude de fonction 39
9 Fonctions trigonométriques 41
9.1 Rappel ...................................... 41
9.2 Dérivée ...................................... 43
10 Optimisation 45
iii

11 Taux relatifs 47
11.1 Notion de différentielle ............................. 47
11.2 Taux relatifs ou taux liés ............................ 49
12 L’intégrale 51
12.1 Primitive ..................................... 51
12.2 Vitesse et accélération ............................. 53
12.3 Aire ....................................... 55
12.4 Théorème Fondamental ............................. 57
12.5 Règles d’intégration ............................... 58
13 Le calcul intégral 63
13.1 Aire entre deux courbes ............................ 63
13.2 La moyenne ................................... 64
13.3 Le volume de révolution ............................ 66
13.4 La longueur d’arc ................................ 66
Bibliographie 69
Index 69
iv

1
Introduction
Quelles sont les racines du calcul différentiel et intégral ?
Elles viennent probablement de Pythagore (environ 500 av J.-C.), plus spécialement d’une
découverte qui l’humilia et le bouleversa :
les nombres entiers sont insuffisants pour bâtir les mathématiques.
(Pythagore prêchait que toute la nature, l’univers entier, toutes choses mathématiques
reposaient sur le modèle discret des nombres entiers : 1, 2, 3, ...) Voilà cette découverte :
le rapport du côté d’un carré à sa diagonale ne peut pas s’exprimer par le rapport de
deux nombres entiers. On ne peut pas trouver deux nombres entiers tels que le carré de l’un
soit égal au double du carré de l’autre. (équivalent : √2n’est pas un nombre rationnel !)
Citons également Archimède (287 à 212 av J.-C.) qui cherchait à déterminer des lon-
gueurs de courbes ou l’aire de surfaces gauches (non planes). Il remarqua que les axiomes
généraux ne suffisaient pas.
Archimède va faire de l’approximation et de l’intégration (cela ne s’appelle pas encore
ainsi). Il est considéré comme le précurseur du calcul intégral (calcul d’aire avec sa mé-
thode d’exhaustion) et différentiel (tangente à des spirales).
Il faudra attendre la fin du XVIIesiècle pour voir éclore le calcul différentiel et intégral
avec Newton (1642 – 1727) et Leibniz (1646 – 1716) qui développent parallèlement et
chacun à leur manière cette nouvelle théorie (1670 – 1700). On ne parle pas encore de limite.
Newton parle de « fluente » et de « fluxion » alors que Leibniz utilise la notion de « nombre
infiniment petit » (cette notion est en contradiction avec la propriété archimédienne des
nombres réels). Voici ce que disait l’évêque Georges Berkley, un contemporain de Newton
et Leibniz : « Que sont ces fluxions ? Les vitesses d’accroissements infiniment petits. Et que
sont ces accroissements infiniment petits eux-mêmes ? Ce ne sont ni des quantités finies,
ni des quantités infiniment petites, pas même rien. Ne pouvons-nous pas les appeler des
fantômes de quantités disparues ? »
Néanmoins, tous les résultats obtenus par Leibniz et Newton étaient corrects et ont été
utilisés jusqu’au milieu du XIXesiècle. Cette contradiction va amener les mathématiciens
de l’époque à rechercher une approche qui permette de la contourner. Il faudra attendre
encore quelques années et la venue des mathématiciens Euler (vers 1750), Cauchy (1821),
Bolzano (1781 – 1848), Weierstrass (1815 – 1897. 1861 : définition rigoureuse de la limite
et en usage depuis) et d’autres pour compléter la théorie des limites en particulier et
du calcul différentiel et intégral en général. Dans les années 1960, des mathématiciens
ont tenté de redonner vie à la notion de nombre infiniment petit (Abraham Robinson,
1