corrigé - résumés de cours , exercices de maths avec corrigés 1S et

Trigo - corrigés feuille d’exercices 1
arcs et angles dans un plan orienté page 1 /10
En préalable : des vocabulaires , des outils dans un plan orienté
1) un triangle ABC est dit de sens direct lorsque les angles orientés \ (! AB; ! AC),\ (! BC; ! BA)\ (! CA; ! CB)associés aux sommets
du triangle ont des mesures principales positives .
!En utilisant le cercle Ccirconscrit au triangle ABC , pour aller de Avers B
puis de Bvers Cpuis de Cvers Aon se déplace sur Cdans le sens direct .
!Les arcs orientés indiquant les mesures ,,des angles \ (! AB; ! AC),
\
(! BC; ! BA)\ (! CA; ! CB)sont orientés dans le sens direct .
!\ (! u ; ! v),\ (! u ; ! v)sont de même mesure ;\ (! i ; ! j),\ (! i ; ! j)sont de même
mesure .
! ! uet ! jétant colinéaires de sens contraires , L’angle orienté \ (! u ; ! j)
est un angle plat de mesure 
!L’angle orienté \ (! u ; ! j)étant un angle plat de mesure , la relation de Chasles
…gure : ABC de sens direct
concernant les mesures des angles orientés permet d’a¢ rmer : ++=
2) un triangle ABC est dit de sens indirect lorsque les angles orientés \ (! AB; ! AC),\ (! BC; ! BA)\ (! CA; ! CB)associés aux sommets
du triangle ont des mesures principales négatives dont la somme vaut . Dans ce cas , pour aller de Avers Bpuis de Bvers C
puis de Cvers Aon se déplace dans le sens indirect sur le cercle Ccirconscrit au triangle ABC . Sur la …gure ci-dessus il
su¢ t de conserver la position de Aet de permuter les sommets Bet Cpour obtenir un triangle ABC de sens indirect et alors
"tout tourne en sens indirect " !
3) Le cercle circonscrit à un triangle ABC rectangle en A est un cercle de diamètre [BC].
4) Le cercle de diamètre [BC]est l’ensemble des points Mtels que ! MB ?! MC ( avec Mdisctinct de Bet C, le triangle MBC
est rectangle en M) .
5) angle opposé de \ (! u ; ! v): avec mesure de \ (! u ; ! v)on a : mesure de \ (! v ; ! u). Autrement dit : (! v ; ! u) (! u ; ! v) [2].
6) angle \ (a! u ; b! v): avec aet bnon nuls : (a! u ; b! v)(! u ; ! v) [2],ab > 0;(a! u ; b! v)+ (! u ; ! v)[2],ab < 0.
7) Relations de Chasles concernant les angles orientés
!avec des vecteurs ! u ; ! v ; ! w ; ! t:8
<
:
(! u ; ! v)(! u ; ! w) + (! w ; v)[2]
(! u ; ! v)(! t ; ! v)(! t ; ! u)[2]
!avec des vecteurs ! OA; ! OB; ! OC; ! OI :8
>
>
<
>
>
:
(! OA; ! OB)(! OA; ! OC) + (! OC; ! OB)[2]
(! OA; ! OB)(! OI; ! OB)(! OI; ! OA)[2]
http://www.math-lycee.com Trigo Feuille d’exos 1 corrigés
1

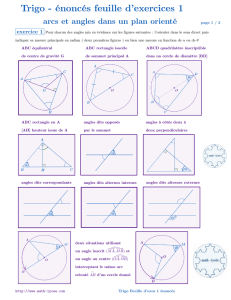
exercice 1 page 2 /10
ABC équilatéral de
centre de gravité G
ABC rectangle isocèle
de sommet principal A
ABCD quadrilatère inscriptible
dans un cercle de diamètre [AB]
ABC rectangle en A
[AH] hauteur issue de A
angles dits opposés
par le sommet
angles à côtés deux à
deux perpendiculaires
angles dits correspondants angles dits alternes internes angles dits alternes externes
deux situations utilisant
un angle inscrit \ (! MA; ! MB)et
un angle au centre \ (! OA; ! OB)
interceptant le même arc
y
AB
A savoir :
(! OA; ! OB)2(! MA; ! MB)[2]
http://www.math-lycee.com Trigo Feuille d’exos 1 corrigés
2

exercice 2 mesures en radians et mesures en degrés page 3 / 10
En préalable
!L’arc orienté
y
II0utilise un demi-tour de longueur et est associé à
l’angle plat \ (! OI; ! OI0)de mesure radians ou bien de mesure 180 degrés .
!Pour les mesures de l’arc orienté
y
IM , qui sont aussi les mesures de
l’angle orienté \ (! OI; ! OM), on utilise le principe suivant pour faire des
conversions degrés ! radians :
mesure de
y
IM = quantité de demi-tour mesure d’un demi-tour
Pour compléter le tableau on commence par déterminer la quantité de demi-tour utilisée ( deuxième ligne du tableau )
radians ; =q1rad 
6rad 1 3= 3
5
9
3
4rad
quantité qde demi-tour utilisée : q=
=d 180
1
'0;32 1 6
60
180 =1 3
100
180 =5 9
3
4
ddegrés ; d=q180 1
180 '57;31 6180 = 30 60o100o3 4180 = 135
radians ; =q7
12 rad  8
34
45
quantité qde demi-tour utilisée : q=
=d 180
7
12
22;5
180 =45 360 =1 8
136
180 =34 45
ddegrés ; d=q180 7
12 180 = 105 22;5o136o
exercice 3 Points images sur un cercle trigonométrique de réels dé…nis par un modulo
le principe On a : 2
nn= 2et donc intuitivement : il su¢ t de faire successivement narcs de cercle de même mesure 2 npour
faire un tour complet du cercle C. En raisonnant modulo n, un ensemble de réels xdé…nis modulo 2
npeut être décomposé en une
partition de ncatégories de réels dé…nis modulo 2et représentés par un seul point image sur le cercle trigo . Un tel ensemble est
donc représenté par un ensemble de nsommets distincts qui sont les extrémités d’un diamètre de C(n= 2) ou bien les sommets
d’un polygone régulier à ncôtés ( n3)
! …gure 1 : points images des réels xtels que : x3
8[]
On a : x3
8[], 9K2Z; x =3 8+K()et avec deux demi-tours (2 )on e¤ectue un tour complet de cercle . En utilisant
les deux restes ( 0et 1) de la division d’un entier par 2on obtient deux formes possibles pour l’entier K:2k+ 0 soit 2k,2k+ 1
D’où : x3
8[], 9k2Z; x =3 8+ 2k ou x=3 8+ (2k+ 1) ()
Puis : x3
8[], 9k2Z; x =3 8+ 2k ou x=3 8++ 2k
Soit : x3
8[], 9k2Z; x =3 8+ 2k ou x=11 8+ 2k
Soit : x3
8[],x 8[2]ou x 11 8[2]
On crée ainsi deux catégories de réels modulo 2associées à deux points
images sur le cercle Cqui sont diamétralement opposés .
entier K0 1 2
x=3
8+K()3
8
3
8+soit : 11 8
3
8+ 2
point image sur CA1A2A1
Pour placer le point A1sur le cercle trigo on utilise : 3
8radians correspond à 3180 8degrés soit à 67;5o
http://www.math-lycee.com Trigo Feuille d’exos 1 corrigés
3

! …gure 2 : points images des réels xtels que : x 2
5[2 3]page 4 / 10
On a : x 2
52 3, 9K2Z; x =2 5+K2 3et avec trois tiers de tour 32 3on e¤ectue un tour complet de cercle .
En utilisant les trois restes ( 0,1et 2) de la division euclidienne d’un entier par 3on obtient trois formes possibles pour l’entier K:
3k,3k+ 1 ,3k+ 2 .
D’où : x 2
52 3, 9k2Z; x =2 5+ 3k2 3ou x=2 5+ (3k+ 1) 2 3ou x=2 5+ (3k+ 2) 2 3
Puis : x 2
52 3, 9k2Z; x =2 5+ 3k2 3ou x=2 5+2 3+ 3k2 3ou x=2 5+ 2 2 3+ 3k2 3
D’autre part : 2
5=6 15 et 2 3=10 15 donc : 2 5+2 3=4 15 et : 2 5+ 2 2 3=2 5+2 3+2 3=4 15 +2 3=14 15
Par conséquent : x 2
52 3, 9k2Z; x =2 5+k(2)ou x=4 15 +k(2)ou x=14 15 +k(2)
Soit : x 2
52 3,x 2 5[2]ou x4 15 [2]ou x14 15 [2]
On crée ainsi trois catégories de réels modulo 2associées à trois points images sur le cercle C.
entier K0 1
x=2
5+K2 3;2
3=10 15 2 52 5+2 3=4 15
point image sur CA1A2
K2 3
x=2
5+ 2 2 3=14 15 2 5+ 3 2 3=2 5+ 2
point image A3A1
Pour placer le point A1sur le cercle trigo avec un rapporteur on utilise :
2
5radians correspond à 2180 5degrés soit à 72o
Les trois points images A1,A2,A3sont les sommets d’un triangle équilatéral de sens direct .
En e¤et : les trois angles au centre Ode Cinterceptant les arcs
y
A1A2,
y
A2A3,
y
A3A1sont de mesure 2
3( on passe d’un sommet
du triangle au suivant en faisant un tiers de tour ) . Par conséquent les trois angles inscrits \ (! A1A2;! A1A3),\ (! A2A3;! A2A1),
\
(! A3A1;! A3A2)interceptant respectivement les arcs
y
A2A3,
y
A3A1
y
A1A2sont tous de même mesure 
3.
! …gure 3 : points images des réels xtels que : x4
9[ 2]
x4
9h 2i, 9K2Z;(!
u ; ! v) = 
9+K 2et 4 2= 2soit : quatre quarts de tour pour e¤ectuer un tour complet de cercle .
Avec les quatre restes ( 0,1,2et 3) de la division d’un entier par 4on obtient pour K:K= 4kou 4k+ 1 ou 4k+ 2 ou 4k+ 3
x4
9h 2i, 9k2Z; x =4 9+ 4k 2ou x=4 9+ (4k+ 1)  2ou x=4 9+ (4k+ 2)  2ou x=4 9+ (4k+ 3)  2
x4
9h 2i, 9k2Z; x =4 9+ 2k ou x=4 9+ 1  2+ 2k ou x=4 9+ 2  2+ 2k ou x=4 9+ 3  2+ 2k
x4
9h 2i, 9k2Z; x =4 9+ 2k ou x=4 9+ 2+ 2k ou x=4 9++ 2k ou x=4 9+3 2+ 2k
D’autre part : 4
9=8 18 ; 2=9 18 ;=18 18 ;3 2=27 18 . Par conséquent :
x4
9h 2i, 9k2Z; x =4 9+ 2k ou x=17 18 + 2k ou x=26 18 + 2k ou x=35 18 + 2k
Ainsi : x4
9h 2i,x4 9[2]ou x17 18 [2]ou x13 9[2]ou x35 18 [2]
On a donc quatre catégories de réels modulo 2associées à quatre points images sur le cercle C.
http://www.math-lycee.com Trigo Feuille d’exos 1 corrigés
4

page 5 / 10
entier K0 1 2
4
9+K 24
9
4
9+ 2=17 18
4
9+=13 9
point image sur CA1A2A3
K2 3
x=4
9+3 2=35 18
4
9+ 4  2=4 9+ 2
point image A4A1
Pour placer le point A1sur le cercle trigo avec un rapporteur on utilise :
4
9radians correspond à 4180 9degrés soit à 80o
Les réels 13
9et 4 9ont une di¤érence égale à : leurs points images respectifs A3et A1sont donc diamétralement opposés .
Les réels 35
18 et 13 18 ont une di¤érence égale à : leurs points images respectifs A4et A2sont donc diamétralement opposés .
Les diamètres [A1A3]et [A2A4]sont portés par des droites perpendiculaires car \ (! OA1;! OA2)et
y
A1A2de même mesure 
2.
Les quatre points images A1,A2,A3,A4sont les sommets d’un carré . Les côtés [A1A2],[A2A3],[A3A4],[A4A1]sont de
même longueur p2comme hypothénuses de triangles rectangles isocèles en Oayant les autres côtés de longueur 1( rayon de C) .
! …gure 4 : points images des réels xtels que : x7
10 [2 5]
x7
10 2 5, 9K2Z;(!
u ; ! v) = 7
10 +K2 5et 52 5= 2( on raisonne par cinquième de tour )
En utilisant les cinq restes ( 0,1,2,3et 4) de la division euclidienne d’un entier par 5on obtient cinq formes possibles pour
l’entier K:5k,5k+ 1 ,5k+ 2 ,5k+ 3 et 5k+ 4 . On peut donc remplacer 9K2Z;(! u ; ! v) = 7
10 +K2 5par : 9k2Z;
x=7
10 + 5k2 5ou x=7 10 + (5k+ 1) 2 5ou x=7 10 + (5k+ 2) 2 5ou x=7 10 + (5k+ 3) 2 5ou x=7 10 + (5k+ 4) 2 5
D’autre part : 7
10 + 5k2 5=7 10 + 2k ;7 10 + (5k+ 1) 2 5=7 10 +2 5+ 5k2 5=11 10 + 2k
7
10 + (5k+ 2) 2 5=7 10 +4 5+ 2k =15 10 + 2k =3 2+ 2k ;7 10 + (5k+ 3) 2 5=7 10 +6 5+ 2k =19 10+ 2k ;
7
10 + (5k+ 4) 2 5=7 10 +8 5+ 2k =23 10+ 2k . Par conséquent :
x7
10 2 5, 9k2Z; x =7 10 + 2k ou x=11 10 + 2k ou x=3 2+ 2k 2 5ou x=19 10+ 2k ou x=23 10+ 2k
x7
10 2 5,x7 10 [2]ou x11 10 [2]ou x3 2[2]ou x19 10 [2]ou x23 10 [2]
entier K0 1 2 3 4 5
7
10 +K2 57
10
11
10
3
2
19
10
23
10
7
10 + 2
point image sur CA1A2A3A4A5A1
Pour placer le point A1sur le cercle trigonométrique de centre Oon
utilise : 7
10 radians correspond à 7180 10 degrés soit à 126o
Les cinq points images A1,A2,A3,A4,A5sont les sommets d’un
pentagone régulier (pentagone ayant 5 angles égaux et cinq côtés de
même longueur ) .
http://www.math-lycee.com Trigo Feuille d’exos 1 corrigés
5