Chute libre et projectiles - Jean

Chute libre et projectiles
I65. Jongleur.
Un jongleur lance une balle vers le haut avec la vitesse v0 ; cette balle atteint sa plus grande hauteur, soit h = 1 m, à
l'instant 0, puis retombe. A ce même instant, le jongleur lance une autre balle, qui monte à la même hauteur que la
première. Où les deux balles se croisent-elles ?
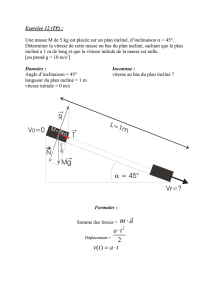
II58. Projectile.
Du point de coordonnées horizontale x = 0 et verticale y = h, on lance un projectile à la vitesse horizontale v0. Ce
projectile n’est pratiquement soumis qu’à son poids, la résistance de l’air étant négligeable. Il touche le sol, qui est
horizontal, au point de coordonnées horizontale x = 2h et verticale y = 0.
1) Déterminer la vitesse v0 de lancement.
2) Déterminer la vitesse 1
v
G
immédiatement avant le choc.
3) Déterminer les modules des composantes normale et tangentielle (par rapport à la trajectoire) de l’accélération
immédiatement avant le choc.
4) Déterminer le rayon de courbure de la trajectoire au point d’impact avec le sol.
5) Le projectile rebondit élastiquement sur le sol : le choc change sa vitesse en la symétrique par rapport au sol.
Déterminer (de préférence intuitivement plutôt que par le calcul) le point d’impact où se produit le deuxième rebond.
6) Si de la même altitude on avait lancé le projectile avec une vitesse de même module et de direction différente, la
distance entre rebonds successifs serait-elle augmentée ou diminuée ? Une argumentation sans calcul sera préférée.
y
0
v
G
β
α
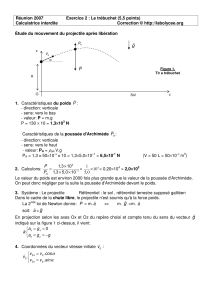
III15. Projectile.
1) Le mouvement d’un projectile est celui d’un corps pesant qui ne subit pas
d’autre force que son poids (en particulier, pas de freinage par l’air). Montrer que
ce mouvement est réversible, c’est-à-dire que si un mouvement
()
rft=
G
G
est
possible, le mouvement
()
rft=−
G
G
est également possible. Que peut-on dire
des positions et des vitesses de ces deux mouvements à l’instant 0 ?
x
2) On lance un projectile avec une vitesse 0
v
G
de module déterminé et faisant
un angle α avec l’horizontale depuis un point situé en bas d’un plan incliné d’un angle sur l’horizontale. Le plan
vertical (P) contenant
β
0
v
G
est perpendiculaire au plan incliné et contient la ligne de plus grande pente de ce plan. On
néglige le freinage par l’air du projectile.
O
Montrer que le mouvement a lieu dans (P).
3) Exprimer la distance D entre le point de départ et le point où le projectile retombe sur le plan incliné en fonction
des coordonnées de la pesanteur et de la vitesse initiale, les axes étant pris suivant la ligne de plus grande
pente du plan incliné et suivant sa normale.
00
,, ,
xy x y
ggv v
4) Montrer que 2
0
2
[sin(2 ) sin ]
cos
v
Dg
−−
=αβ β
β.
5) Montrer que la portée maximale s’obtient en tirant dans la direction de la bissectrice de la ligne de plus grande
pente du plan incliné et de la verticale.
6) Le projectile rebondit élastiquement sur le plan incliné, qui change sa vitesse en la symétrique par rapport au plan
incliné. Il existe un cas simple où le projectile après avoir rebondi sur le plan incliné revient à son point de départ. Quel
est ce cas simple ? On ne demande pas de discuter si ce cas est le seul. Montrer que l’angle de tir nécessaire satisfait à
1
tan( ) 2tan −=αβ β.
7) Le projectile rebondit élastiquement deux fois sur le plan incliné. Chaque rebond élastique change la vitesse en sa
symétrique par rapport au plan incliné. Il existe un cas simple où le projectile après avoir rebondi deux fois sur le plan
incliné revient à son point de départ. Quel est ce cas simple ? On demande de répondre à cette question sans aucun
calcul.
Réponses
I. 12
30, 75 m
4
zz h== = .
II. 1) 02vg=h0
v v==− ; 2) vv ; 3)
10 1
;
xy /2 n
t
aa ; 4) g== 42R; 5) abscisse 6 ; h=h
6) diminuée.
III. 1) même position vitesse opposée ; 3) 0
0
2
2(
y
xy yx
y
v
Dgvg
g
=−0 )v
; 6) si le mobile frappe le plan incliné avec une
vitesse perpendiculaire à ce plan ; 7) après le premier rebond le projectile monte verticalement.
Chute libre et projectiles, page 1

Corrigé
I.
D’après le théorème de l’énergie cinétique, 2
0
2
0
1
022
v
mv mgh h g −=−⇒=.
2
1
12
2
1
20
2
2
1
12 0 12 20
30, 75 m
4
zgth
zgtvt
h
zz hvtzzhg h
v
=−+
=−+
⎛⎞
⎟
⎜
=⇔=⇒==−==
⎟
⎜⎟
⎜
⎝⎠
II. 1) 2
1
02
;xvt y gt h==−+.
Au point de chute, , 0y=2h
tg
=, 00
222 h
xv h v gh
g
==⇒=
2)
00
11
;
xy
vv v gt==−=−v
3) ag=
G
G fait un angle de 45° avec 1
v
G
, donc /2
n
t
aa g==
4) 22
10
242
2
n
vv
g
aR
RR
===
h
5) Le second rebond a lieu à l’abscisse 6. h
6) On ne change pas le module de la vitesse d’impact, mais seulement sa direction ; or la direction actuelle ( 1
v
G
incliné à 45°) est celle qui donne la plus grande portée, donc un changement de direction implique une distance entre
rebonds plus petite.
III.
1)
()
22
1
00
2
2
dr dr
ggtvrftgtvt
dt
dt =⇒=+ = = + +
0
r
G
G
G
G
G
G
GG G G
. Le mouvement
()
2
10
2
rft gtvtr=−=−+0
G
G
G
GG
est
un mouvement possible, pour lequel à l’instant 0 la position 0
r
G
est la même et la vitesse est l’opposé 0 v−
G
.
2) 22
1
0
2
2
dr dr
ggtvrgt
dt
dt =⇒=+ = +
0
vt
G
G
G
G
GGGG
qui montre que le mouvement a lieu dans le plan (P).
3) Les équations du mouvement sont :
2
1
20
2
1
20
xx
yy
xgtv
ygtv
=+
=+
t
t
Le mobile retombe quand
2
0000
11
00
22
2
2222
()0 (
yyyy
yy x x xyy
yyyy
vvvv
ygtvt t xg v gvgv
gggg
⎛⎞
⎟
⎜
=+==−=−=−
⎟
⎜⎟
⎟
⎜
⎝⎠ 00
)
x
.
4)
00 0
2 2
0 0
22
cos( ) sin( ) sin cos
2 sin( )[ sin sin( ) cos cos( )] 2 sin( )cos
cos cos
xoyxy
vv vv g g g g
vv
Dx gg
=−=−=−=−
−− −+−−
== =
αβ αβ β β
αβ β αβ β αβ αβ α
ββ
car
Or
cos( ) cos cos sin sinab a b a b+= −
1
2
sin cos [sin( ) sin( )]ab ab ab=++−
2
0
2
[sin(2 ) sin ]
cos
v
Dg
−−
=αβ β
β
5) D est maximum quand 1
22
sin(2 ) 1 2 ( )
2
π
π
αβ αβ α β−=−==+
qui exprime que 0 v
G
est dirigé selon la
bissectrice de la verticale et de la ligne de plus grande pente du plan incliné.
6) Soit M le point d’impact. Si le mobile frappe en M le plan incliné avec une vitesse perpendiculaire à ce plan, le
choc change la vitesse 0
v
G
en son opposé 0 v−
G
. Choisissons l’instant du choc comme origine des temps. Le mouvement
2
1
20
rgtv=−t
G
G
G après le choc se déduit du mouvement 2
1
20
rgtv=+t
G
G
G avant le choc en remplaçant t par puisque
le mouvement des projectiles est réversible. Le projectile revient donc au point de départ en un temps égal au temps de
l’aller.
t−
Chute libre et projectiles, page 2

On peut montrer que c’est le seul cas où il y ait retour à l’envoyeur. En effet, si la vitesse en A n’est pas
perpendiculaire au plan incliné, alors l’aller et le retour ont mêmes trajectoires que deux lancers de A avec même et
des opposés ; ces deux mouvements ont même loi et même instant de retombée
0y
v
0x
v()yt 0 2/
y
y
vg ; leur abscisse de
retombée 2
1
20
xx
xgtv=+t est fonction croissante de ; comme ces deux mouvements correspondent à des valeurs
opposées de , la retombée a lieu en des endroits différents si .
0x
v
0x
v00
x
v≠
Calculons l’angle de tir. En M :
000
00 0
0
22 1
0tan()
22
x
yyyy
xx x
xx x
yy x
x
vgvv
g
vv gtv g v
ggvg
αβ β =+=−=−=⇒=−=tan
.
7) Ce cas simple est celui où après le premier rebond le projectile monte verticalement.
Chute libre et projectiles, page 3