Lois à densité

Lois à densité
1. Variable aléatoire suivant une loi à densité
Idésigne un intervalle (borné ou non) de R
Définition
On appelle densité de pro-
babilité sur Itoute fonction fdé-
finie sur Itelle que :
1) fest continue et positive sur I
2) L’aire sous la courbe Cde fest
égale à 1 u.a.
Définition
fdésigne une densité de pro-
babilité sur I.
Une variable aléatoire Xsuit la loi
de densité fsi, pour tout intervalle
Jinclus dans I, la probabilité de l’événement X∈Jest donnée par :
p(X∈J) = Aire(D)où Dest le domaine sous la courbe Csur l’intervalle J
Si J= [a;b],p(X∈J) = Zb
a
f(x)dx
On dit aussi que Xest une variable aléatoire continue de densité f.
2. Propriétés
Pour tous réels aet bde I:
1) p(X=a) = 0
2) p(X > a) = 1 −p(X≤a)et p(a < X < b) = p(X < b)−p(X≤a)
3. Espérance mathématique
Soit Xune variable aléatoire continue de densité fsur l’intervalle [a;b]alors l’espérance
mathématique de Xest le réel défini par :
E(X) = Zb
a
tf(t)dt
4. Exercice
1) Soit fla fonction définie sur l’intervalle [0; 10] par : f(x) = 0,006(10x−x2).
Vérifier que fest une densité de probabilité sur [0; 10].
2) Soit Xune variable aléatoire continue ayant fpour densité de probabilité.
Calculer : p(X≤7) et p(X > 6)
3) Calculer l’espérance mathématique E(X)
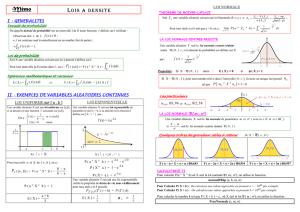
5. Loi uniforme sur [a ; b]
(a) Définition Soit aet bdeux nombres réels tels que a < b.
La loi uniforme sur [a ; b] est la loi ayant pour densité de probabilité la fonction
constante fdéfinie sur [a;b]par : f(x) = 1
b−a
(b) Propriétés
1) Pour tout réel xappartenant à [a;b]:p(a≤X≤x) = x−a
b−a
2) E(X) = b+a
2
Démonstrations Exercice
1

6. Loi exponentielle
(a) Définition
Une variable aléatoire continue Tsuit une loi exponentielle de paramètre le réel
λ > 0si sa densité de probabilité est la fonction fdéfinie sur [0; +∞[par :
f(x) = λe−λx
Dans ce cas,on a pour t > 0:
p(T≤t) = Zt
0
λe−λxdx =−e−λxt
0= 1 −e−λt
p(T > t) = e−λt
(b) Remarque (ROC) F
Si Tsuit la loi exponentielle de paramètre λalors, pour tout t≥0et h≥0, on a :
pT≥t(T≥t+h) = p((T≥t+h)∩(T≥t))
p(T≥t)=p(T≥t+h) p(T≥t)=e−λ(t+h) e−λt =e−λh =p(T≥h)
On dit que Tsuit une loi de durée de vie sans vieillissement c’est-à dire, si, par
exemple, Tdonne la durée de vie d’un appareil en années alors, sachant qu’il a déjà fonctionné
tannées, la probabilité qu’il fonctionne hannées supplémentaires est la même que la probabilité
qu’il fonctionne au moins hannées à partir de sa première mise en fonction.
(c) Espérance mathématique
Soit Xune variable aléatoire qui suit une loi exponentielle de densité f.
On définit l’espérance mathématique de Xpar :
E(X) = lim
t→+∞Zt
0
xf(x)dx
(d) Propriété
Soit Xune variable aléatoire qui suit une loi exponentielle de paramètre λ > 0.
Alors : E(X) = 1
λ
Démonstration(ROC) F
Soit t≥0.
Pour tout x≥0,xe−λx0=e−λx −λxe−λx
Donc : Zt
0
xλe−λxdx =Zt
0
e−λxdx −Zt
0xe−λx0dx
=−e−λx
λt
0−xe−λxt
0
=1
λ−e−λt λ−te−λt
Quand ttend vers +∞, on obtient : E(X) = 1
λ
2

7. Loi Normale
(a) Loi normale centrée réduite
Une variable aléatoire continue Xsuit
la loi normale centrée réduite si sa den-
sité fest définie sur Rpar :
f(x) = 1
√2πe−
x2
2
On note : Xsuit la loi N(0; 1).
(b) Remarque
La fonction fest paire donc sa courbe est symétrique par rapport à l’axe des ordonnées.
On dit que cette courbe est une courbe en cloche ou courbe de Gauss.
(c) Propriétés
Soit Xest une variable aléatoire qui suit la loi N(0; 1)
i. Pour tout nombre réel u:
p(X≤ −u) = 1 −p(X≤u)
Démonstration
Par symétrie de la courbe en cloche
par rapport à l’axe des ordonnées,
p(X > −u) = p(X≤u)et donc :
p(X≤ −u) = 1 −p(X≤u)
ii. Pour tout nombre réel α∈]0; 1[, il existe un unique nombre réel positif uαtel que :
p(−uα≤X≤uα) = 1 −α
Démonstration (ROC) F
Pour tout réel tpositif, p(−t≤X≤t) = 2p(0 ≤X≤t) = 2 Zt
0
f(x)dx = 2G(t)
où Gest la primitive de fsur Rqui s’annule en 0. La fonction 2Gest continue et strictement
croissante sur [0; +∞[. On a le tableau de variation ci-dessous :
t0+∞
2G
0
1
Si α∈]0; 1[,1−αaussi.et d’après le corollaire du théorème des valeurs intermédiaires, il
existe un unique réel positif uαtel que 2G(uα) = 1 −α=p(−uα≤X≤uα)
iii. Cas Particuliers à connaître
Pour α= 0,05 une valeur approchée de u0,05 est 1,96
Pour α= 0,01 une valeur approchée de u0,01 est 2,58
u0,05 = 1,96 soit p(−1,96 < X < 1.96) ≈0,95
u0,01 = 2,58 soit p(−2,58 < X < 2,58) ≈0,99
iv. L’espérance mathématique de Xest 0 et sa variance est 1 où la variance de Xest
définie par : V(X) = E((X−E(X))2)
3

(d) Loi Normale Générale
Soit µun nombre réel et σun réel strictement positif.
Une variable aléatoire Xsuit la loi normale de paramètres µet σ2si le variable aléatoire
Z=X−µ
σsuit la loi normale N(0; 1).
On dit alors que Xsuit la loi N(µ;σ2)
i. Propriété Si Xsuit la loi N(µ;σ2)alors son espérance est µet sa variance σ2
ii. Trois valeurs à connaître
Xsuit la loi N(µ;σ2)
*p(µ−σ < X < µ +σ)≈0,68
*p(µ−2σ < X < µ + 2σ)≈0,95
*p(µ−3σ < X < µ + 3σ)≈0,99
Exercice Vérifier ces résultats à l’aide de votre calculatrice.
iii. Théorème de Moivre-Laplace
Xnest une variable aléatoire qui suit la loi B(n;p)et Znla variable aléatoire
Zn=Xn−E(Xn)
σ(Xn)=Xn−np
pnp(1 −p)
Pour tous nombres réels aet bavec a≤bet si fla densité de probabilité de la loi normale
centrée réduite alors
lim
n→+∞p(a≤Zn≤b) = Zb
a
f(t)dt
iv. Exemple n= 36, p = 0,5donc np = 18, σ =√9 = 3
v. Remarque
Si on a n≥30, np ≥5, n(1 −p)≥5la loi binomiale B(n;p)est très proche de la loi
normale de même espérance np et de même variance np(1 −p)
C Gerlein Maths Outils