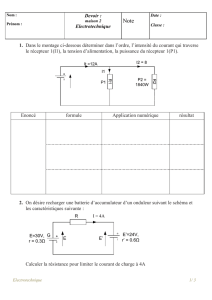
[ ] ] [ COMPLEXES : EXERCICES

1) Dans le plan complexe, dans chaque cas, représenter l’ensemble des points M d’affixe z tels que :
a) b) Im 2z=5=zIm c) 2zi
−
=
2) Répondez aux questions suivantes, en utilisant rapidement une représentation graphique
a) Si z
′=z, que peut-on dire de z′ et de arg(z’) en liaison avec z et de arg(z) ?
b) Si , que peut-on dire de z
′=−zz′ et de arg(z’) en liaison avec z et de arg(z) ?
c) Si , que peut-on dire de zi
′=zz′ et de arg(z’) en liaison avec z et de arg(z) ?
Dans le plan complexe, dans chaque cas, préciser l’ensemble des points M d’affixe z tels que :
a) 21ziz+=−+3i b) où 2ix
ze=;
2
x
π
π
∈
 c)
[
2) 2
22
zi
z
]
arg(
π
π
−
=
+
d) a étant un réel positif fixé , 0avec
i
zz ae
θ
=+
]
[
0,
θ
π ∈
i
Résoudre dans les équations suivantes ^
a) où a>0 b) c) 0
22 =+ az 21z=+ 35z
=
d) z38
=
− e)
4
zi=
1) Calculer le module de a) b)
5
1(3 2 )z=+i2
11
11
zii =−
2
+
−
2) Soit , exprimer en fonction dezxiy=+
x
et de y le module de 2
31zz
=
− et celui de 4
1
1
zz =−
Exercice C1 : (N0 ) Enoncé
Exercice C2 : (N1 ) Enoncé
Exercice C3 : (N1 ) Enoncé
Exercice C4 : (N0 ) Enoncé
Exercice C5 : (N1 ) Enoncé
COMPLEXES : EXERCICES
Déterminer le module et un argument des nombres complexes suivants :
a) (donner une valeur approchée de la mesure en degrés de l’angle (,
12z=− −i11
OM)e
J
JJJJG
G
où (
1
M12zi
=
−−) )
a) où ze
i
2=
α
α
∈
R
b) 33i ze
α
=− où
α
∈
R
d)
][
ze
i
41=+ ∈
θ
θππ , - ,
1
(indication : écrire z (...) 22
4′
×=×=
θθ ii eez puis exprimer
′
zen fonction de 2
deet
2
cos
θθ
sin )

Déterminer la valeur des complexes suivants (plusieurs cas peuvent être envisagés pour chaque question)
(pensez à vous aider d’un dessin)
a) ( )
ik
k
ze k
π
=∈] b) ()
2 ( )
ik
k
ze k
π
π +
=∈]
Linéariser 3 sin
x
et 4 cos
x
(c’est à dire exprimer ces expressions en sommes ou différences de termes de type cos ou ) kx sin kx
Remarque : la linéarisation est notamment utile pour intégrer
On considère l’ équation (e) :
32
(2 2) (5 4) 10 0zizizi++ +− − =
Montrez que (e) admet une solution imaginaire pure, puis résoudre (e)
0
1) Soit . Préciser la transformation géométrique qui, à tout point M d’affixe z fait correspondre M’( ’) tel
que
00
zaib=+
0
zzz=+
z
′
2) Soit k un réel non nul. Préciser la transformation géométrique qui, à tout point M d’affixe fait correspondre M’( ’) tel que
z z
zkz
′=
Résoudre dans les équations a) ^ziz )31(
2+= b) 02)cos2( 212 =+− +
θθ
θ zz
Déterminer la forme cartésienne de z= ix
ix
e
e
+
−
1
1pour
π
kx
≠
()Zk
∈
Exercice C6 : (N2 ) Enoncé
Exercice C7 : (N1 ) Enoncé
Exercice C8 : (N1 ) Enoncé
Exercice C9 : (N1 ) Enoncé
Exercice C10 : (N1 ) Enoncé
Exercice C11 : (N1 ) Enoncé
Exercice C12 : (N1 ) Enoncé
Soit j= 3
2 π
i
e 1) préciser les valeurs de ;
3jj et 1 2
jj ++
2) Simplifier puis donner module et argument de et de )1)(1( 2
1jjz −−= ))(1( 2 2jjjz −−=
2

Soit 3
4
1
)(
z
zf = 1) Résoudre dans C l’équation . Soient et les deux solutions de parties
imaginaires positives. 2) Calculer
01
4=+z1
z2 z
)()( 21 zfzf +
2) = )()( 21 zfzf +3
2
3
14
1
4
1
zz
+=4
2
2
4
1
1
44 z
z
z
z+=)(
4
1
21 zz +
−=4
2i−
Exercice C13 : (N1 ) Enoncé
Exercice C14 : (N2 ) Enoncé
Montrer que si 2
θ
π ∉] alors
)
2
sin(
)
2
1
sin(
2
0
θ
θ
θ
θ
+
=
∑
=
n
ee in
n
k
ik
3