Irrationalité de /2 - Page personnelle de Baptiste GORIN

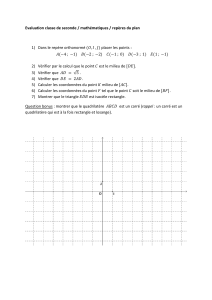
Irrationalité de √2
Baptiste GORIN
Théorème. — √2est irrationel.
Démonstration
Première démonstration. — Supposons par l’absurde que √2est un nombre rationnel. Il existe alors p, q ∈N∗
premiers entre eux tels que √2 = p
q. Alors p2= 2q2. Par suite, pest divisible par 2:p= 2p′. Donc 2p′2=q2.
qest alors également divisible par 2. On aboutit à une contradiction.
Deuxième démonstration. — Supposons par l’absurde que √2est un nombre rationnel. Il existe alors p, q ∈N∗
tels que √2 = p
q. Alors p2= 2q2. En considérant les décompositions en facteurs premiers de pet q, on constate
que p2et q2ont un nombre pair de facteurs premiers. Comme 2q2a un nombre impair de facteurs premiers, on
aboutit à une contradiction.
Troisième démonstration. — Supposons par l’absurde que √2est un nombre rationnel. Il existe alors m∈N∗,
minimal, tel que m√2soit un entier. Considérons n=m(√2−√2) = m(√2−1). Notons que nest un nombre
entier tel que 06n < m. De plus n√2 = 2m−m√2est un entier. Le caractère minimal de massure alors que
n= 0. Par suite √2 = √2= 1. On aboutit à une absurdité.
Quatrième démonstration. — Par le théorème de Pythagore, un triangle rectangle isocèle dont les côtés de l’angle
droit ont pour longueur 1a une hypoténuse égale à √2. Donc, si √2est rationnel, avec √2 = p
q,p, q ∈N∗,
l’image d’un tel triangle rectangle par une homothétie de rapport qest un triangle rectangle isocèle dont les
longueurs des trois côtés sont des nombres entiers. Par suite, il doit exister un plus petit triangle rectangle
isocèle ayant cette propriété. Mais, à l’intérieur d’un triangle rectangle isocèle dont les longueurs des côtés sont
des nombres entiers, on peut toujours construire un plus petit triangle ayant les mêmes propriétés :
Par suite, √2ne peut pas être rationnel.
Cinquième démonstration. — Supposons par l’absurde que √2est un nombre rationnel. Il existe alors p, q ∈N∗,
avec qminimal, tels que √2 = p
q. On a p > q et q > p −q. De plus :
2q−p
p−q=
2−p
q
p
q−1=2−√2
√2−1=√2
Ceci contredit le caractère minimal de q.
Sixième démonstration. — Considérons l’ensemble E = {a+b√2; a, b ∈Z}.Eest fermé et stable pour l’addition
et la multiplication.
Considérons α=√2−1∈E. Pour tout n∈N,αn∈Ede sorte qu’il existe an, bn∈Ztels que αn=an+bn√2.
Si √2est rationnel, il existe alors p, q ∈N∗tels que √2 = p
q. D’où :
αn=an+bn√2 = anq+bnp
q>1 q
Or, comme α∈]0; 1[, on a lim
n→+∞
αn= 0. On aboutit à une contradiction.
Septième démonstration. — Supposons par l’absurde que √2est un nombre rationnel. Il existe alors p, q ∈N∗
premiers entre eux tels que √2 = p
q.
Alors √2nqest un nombre entier pour tout n∈N. En effet
√2nq=2n
2qsi nest pair
2n−1
2psi nest impair

Irrationnalité de √2
On en déduit que
(√2−1)nq=
n
X
k=0 n
k(−1)n−k√2k
q∈N∗pour tout n∈N.
Or, comme √2−1∈]0; 1[, on a lim
n→+∞(√2−1)nq= 0.
On aboutit à une contradiction.
Huitième démonstration. — Supposons par l’absurde que √2est un nombre rationnel. Il existe alors p, q ∈N∗
avec qminimal tels que √2 = p
q.
Alors le carré de côté de pa la même aire que deux carrés de côté q.
= +
Plaçons les deux carrés de côté qà l’intérieur du carré de côté pen deux sommets opposés. Trois carrés dont
les côtés sont entiers apparaissent.
Les deux carrés situés en deux sommets opposés sont égaux et la somme de leur aire est égale à l’air du troisième
carré.
= +
Ceci contredit le caractère minimal de q.
C.Q.F.D.