Sciences Industrielles pour l`Ingénieur

CPGE TSI – Lycée P.-P. Riquet – St-Orens de Gameville - 1 -
Sciences Industrielles pour l’Ingénieur
1 - GENERALITES SUR LA CONVERSION D'ENERGIE ELECTRIQUE EN ENERGIE MECANIQUE : TRANSFERTS
D'ENERGIE EN REGIME TRANSITOIRE (= DYNAMIQUE) ET PERMANENT (= ETABLI)
• Les développements actuels en robotique (machines outils, robots,
manipulateurs …) et en variation de vitesse (TGV, voiture électrique,
entraînements de toute sorte) nécessitent la réalisation d'ensembles
machine - alimentation - commande, qui optimisent les
performances statiques et dynamiques des machines électriques
utilisées en actionneurs.
• La conception de ces ensembles repose sur une approche pluridisciplinaire
qui intègre les bases variées du génie électrique, de l'électrotechnique à
l'automatique, en passant par l'électronique de puissance et l'informatique
industrielle sans oublier la mécanique.
Cette complémentarité s'avère nécessaire à l'optimisation des chaînes
d'entraînement et à l'amélioration des performances des actionneurs
électriques.
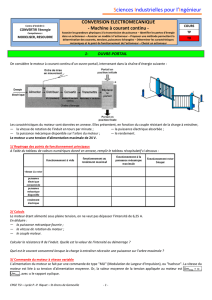
1/ Chaîne de transfert de l'énergie
• De l'énergie électrique
(alternative ou continue) est
distribuée jusqu'à un
convertisseur statique de
puissance (variateur) dont le
rôle est de moduler l'énergie
électrique fournie au moteur
d'entraînement.
• Celui-ci convertit cette énergie électrique en énergie mécanique, qu'il transmettra par l'intermédiaire de son arbre, via un
adaptateur mécanique (réducteur par exemple), aux organes mécaniques entraînés (charge).
• On parle de chaîne de transfert direct de l'énergie lorsque la charge est résistante : c'est le cas par exemple des engins de levage
dans la phase de montée de la charge, où la pesanteur s'oppose au déplacement.
• On parle de chaîne de transfert inverse de l'énergie lorsque la charge est entraînante : c'est le cas, par exemple, des engins de
levage dans la phase de descente de la charge, où la pesanteur agit dans le sens du déplacement. Le moteur entraîné par la charge
mécanique devient générateur et convertit l'énergie mécanique transmise en énergie électrique. Celle-ci est soit stockée dans des
condensateurs, soit dissipée dans des résistances, soit restituée à la source d'énergie électrique (réseau …) par l'intermédiaire du
variateur.
Rapport de réduction :
réd
k
< 1
Réseau EDF
Batterie
Variateur
consignes
limites
mesures
Moteur
Réducteur
Cm
Cr
Arbre
moteur
réd
Charge
Chaîne de transfert direct de l’énergie
Chaîne de transfert inverse de l’énergie
k
Centre d’Intérêt 6 :
CONVERTIR l'énergie
Compétences :
MODELISER, RESOUDRE
CONVERSION ELECTROMECANIQUE
- Machine à courant continu en régime dynamique –
Procédés de pilotage en vitesse et en couple
Associer les grandeurs physiques à la transmission de puissance – Identifier les pertes d'énergie
dans un actionneur – Associer un modèle à l'actionneur – Proposer une méthode permettant la
détermination des courants, tensions, puissances échangées – Déterminer les caractéristiques
mécaniques et le point de fonctionnement de l'actionneur – Choisir un actionneur
TP
COURS 2
TD
MCC ou MAS ou MS

CPGE TSI – Lycée P.-P. Riquet – St-Orens de Gameville - 2 -
Sciences Industrielles pour l’Ingénieur
2/ Les différentes phases du mouvement d’une machine
• La plupart des mouvements, contrôlés par des moteurs, suivent le
cycle simple constitué par l'enchaînement de trois phases élémentaires :
- une phase d'accélération lors du démarrage ;
- une phase de régime établi ou permanent lorsque la vitesse est
stabilisée ;
- une phase de décélération lors du ralentissement pendant l'arrêt.
3/ Caractéristiques mécaniques des charges entraînées
• Le couple résistant, noté Cr, est le couple s’opposant au mouvement d’entraînement de la machine.
• La caractéristique mécanique Cr = f(), où  est la vitesse angulaire du moteur en rad/s, définit les besoins de la charge entraînée.
Il existe essentiellement trois familles de caractéristiques :
• On a représenté, en pointillés, les surcouples résistants opposés par bon nombre de mécanismes au début du démarrage (on dit
au "décollage"). Ce surcouple peut, pour un même mécanisme, être très variable. Mal quantifié lors de l’étude du mouvement, il
peut, s’il est important, empêcher le démarrage ou rendre la mise en vitesse très longue.
4/ Couple à fournir par le moteur
• Ce qui conditionne le bon fonctionnement d’une chaîne d'énergie, c’est la capacité du moteur à fournir à tout instant l’effort
nécessaire, pour permettre le mouvement désiré. Cet effort, imposé au niveau de l’arbre d’entraînement, est le couple moteur,
noté Cm.
Equation générale de la dynamique (PFD)
• L’équation générale de la dynamique s’écrit :
Rq importante : Cr intègre le couple résistant opposé par la charge entraînée ainsi que les couples de frottement divers.
Détermination du moment d’inertie total J ramené sur l’arbre moteur
• La conservation de l’énergie cinétique impose :
W = W'
2
réd
éq ch
Ω
J = J . Ω
2
éq ch
J = J .k
On en déduit l’expression du moment d’inertie total ramené sur l’arbre moteur :
• Le moment d’inertie de la charge est donc ramené sur l’arbre du moteur, affecté d’un coefficient k².
Comme k est inférieur à 1 dans le cas d’un réducteur, k² << 1.
 (rad/s)
t
accélération
régime établi
décélération
- ventilateurs,
- pompes, …
Cr
- bobineuses,
- tours, …
r
K
C=
Ω
Cr
- engins de levage,
- convoyeurs, …
ste
r
C = C
Cr
2
r
C = K.Ω
Surcouple
au "décollage"
Energie cinétique
de la charge :
Moteur
Cm
Cr
Charge équivalente
moment d’inertie Jéq
Energie cinétique de
la charge équivalente :
Moteur
Réducteur
Cm
Cr
réd
k
Charge
moment d’inertie Jch
Moment
d’inertie Jm
On compte positif le couple résistant Cr qui s'oppose au
couple moteur, conformément aux courbes ci-dessus.

CPGE TSI – Lycée P.-P. Riquet – St-Orens de Gameville - 3 -
Sciences Industrielles pour l’Ingénieur
Régimes de fonctionnement
• Le mouvement d’une charge, contrôlé par un moteur, est caractérisé par 2 régimes de fonctionnement :
- le régime établi ou permanent ;
- le régime transitoire : accélération et décélération.
Accélération
Lors des phases de montée en vitesse, on a :
dΩ>0
dt
Compte tenu de l’équation générale de la dynamique, il faut que : Cm > Cr
On appelle
a
dΩ
C = J. dt
le couple accélérateur, ou couple d'inertie, nécessaire pour
vaincre l’inertie s’opposant à la variation positive de vitesse.
Accélération
Régime établi
Le régime est établi lorsque la vitesse est constante :
dΩ=0
dt
L’équation générale de la dynamique se réduit à : Cm = Cr
Il y a équilibre dynamique, correspondant à l’égalité entre le couple moteur et le
couple résistant.
Régime établi
Décélération
Lors des phases de ralentissement, on a :
dΩ<0
dt
On définit le couple de ralentissement par :
ral
dΩ
C = -J. > 0
dt
Trois cas peuvent se présenter :
 : 1/ Décélération naturelle
Le moteur n’est plus alimenté  Cm = 0
ral 1 r
dΩ
C = -J. = C
dt
 : 2/ Décélération lente
Le moteur développe un couple mécanique
"moteur" pour éviter un arrêt prématuré.
ral 2 r m ral 1
dΩ
C = -J. = C - C < C
dt
 : 3/ Décélération rapide
Le moteur développe un couple mécanique "résistant", renforçant celui produit
par la machine  Cm = - Cf (couple de freinage ; exemple : voir plus loin "Pilotage
de la MCC" 2/)
ral 3 r f ral 1
dΩ
C = -J. = C + C > C
dt
Décélération
naturelle
Décélération
lente
Décélération
rapide
Fonctionnement stable du moteur
• On détermine le point de fonctionnement M en régime établi du groupe moteur - charge entraînée en représentant sur un même
diagramme les caractéristiques mécaniques du moteur Cm = f() et de la charge Cr = f() qu’il entraîne.
En effet, en régime établi ( = Cste), on a :
mr
dΩ
J. = C - C = 0
dt
mr
C = C
• D'une manière générale, le groupe est en régime stable lorsque toute modification de l'une des variables qui fixent son régime
entraîne une action correctrice qui tend à rétablir le régime initial : supposons par exemple que, pour une cause extérieure, le
groupe ralentisse. Il y a deux possibilités :
Cm
Cr
Cr
Cm
Cr
Cf
Cr
t
Cm > 0
Cr > 0
 > 0
> 0
< 0
> 0

CPGE TSI – Lycée P.-P. Riquet – St-Orens de Gameville - 4 -
Sciences Industrielles pour l’Ingénieur
• Pour qu’il y ait stabilité, il faut qu’au voisinage de l’intersection, on ait :
mr
dC dC
<
dΩ dΩ
5/ Quadrants de fonctionnement
• Généralement, un mécanisme a besoin de 2 mouvements de sens opposés, obtenus par inversion du sens de marche du moteur
d’entraînement. De plus, il est souvent nécessaire d’obtenir un temps d’arrêt du mouvement plus court que celui obtenu
naturellement, ce qui nécessite un couple de freinage.
• Il existe donc, pour un moteur accouplé à une charge, plusieurs
zones de fonctionnement ou quadrants de fonctionnement (cf. cours
précédent). Les divers fonctionnements sont caractérisés par :
- une marche en MOTEUR dans les quadrants 1 et 3 : Cm et Ω de
mêmes signes.
- une marche en FREINAGE dans les quadrants 2 et 4 : Cm et Ω de
signes contraires.
6/ Exemple de cycle de fonctionnement
• On étudie le mouvement horizontal d’une charge, entraînée par
un moteur. Le couple résistant est constant et vaut :
Cr0 (> 0) si  > 0
-Cr0 si  < 0
Son allure est indiquée à la figure 3. En régime établi, la machine
fonctionne en moteur (quadrant 1 ou 3).
• Le profil de vitesse  = f(t) adopté pour le moteur est donné à la
figure 1.
• On commence par tracer l’allure du couple d’accélération Ca en
fonction du temps. Elle est représentée à la figure 2.
• Pour tracer celle du couple moteur Cm sur tout le profil de vitesse,
il suffit d’ajouter Cr au graphe précédent. En effet :
m r a r
dΩ
C = J. + C = C + C
dt
C'est dans le signe de cette addition que se joue le comportement
moteur ou génératrice de la machine.
Le résultat du tracé est fourni figure 4.
 < n  Cm > Cr 
dΩ>0
dt
   n
Le groupe revient à sa vitesse initiale.
 < n  Cr > Cm 
dΩ<0
dt
   0
Le groupe va finir par s’arrêter.
0
0
t
J
t
0
- 0
20
t0
t0
t0
t0/2
t1
dt
d
JCa
t
0
0
t
J
t
Cr
- Cr0
t
Cm
- Cr0
Cr0
0
0
t
J
0
0
t
J
figure 1
figure 2
figure 3
figure 4
A
B
C
1
0
t2
J
+ Cr0
Cr
Cm
n
Cn
C (Nm)
 (rad/s)
M
 : emballement
 : arrêt
Point de
fonctionnement
INSTABLE
Point de
fonctionnement
STABLE
Cm
Cr
n
Cn
C (Nm)
 (rad/s)
M

CPGE TSI – Lycée P.-P. Riquet – St-Orens de Gameville - 5 -
Sciences Industrielles pour l’Ingénieur
• Enfin, on a représenté à la figure 5, dans le plan Cm(), le
déplacement du point de fonctionnement du moteur pour
obtenir le profil de vitesse.
• On peut distinguer les déplacements instantanés et les
déplacements ayant une durée non nulle, en traçant les premiers
en traits pointillés ( ) et les seconds en traits pleins ( ). On
note A, B et C les points de fonctionnement en régime établi.
• Conclusion
On constate que le moteur travaille dans les quatre quadrants du
plan Cm().
Ce fonctionnement ne sera possible que si la chaîne cinématique
et le variateur de vitesse sont réversibles.
2 - APPLICATION AU COMPORTEMENT D'UN MOTEUR A COURANT CONTINU EN REGIME TRANSITOIRE
(assimilable à un système du 1er ordre)
On étudie le cas d’un moteur à courant continu à excitation séparée et flux constant (ou un MCC à aimants permanents).
1/ Régime transitoire électrique
• Ce régime transitoire est décrit par l'équation différentielle :
di
u = L. + R.i + E
dt
, avec
E = k.Ω
, soit :
di
u - k.Ω = L. + R.i
dt
, qui donne sous la forme canonique :
• Au démarrage, on peut considérer que le terme
(u - kΩ) / R
évolue lentement du fait de l’inertie du
moteur. C’est donc un régime transitoire électrique qui apparaît en 1er avec une constante de temps :
Cette e intervient à chaque changement brutal de i, donc à chaque changement de Cm.
2/ Régime transitoire mécanique
• On sait que lorsqu'on ne néglige pas le couple de pertes, l'équation de la dynamique est :
mr
C - C = J . dΩ / dt
avec : Cm = k.i = couple électromagnétique en N.m ;
J = moment d'inertie des charges en rotation, ramené sur l'arbre moteur ;
Cr = couple résistant total en N.m, incluant le couple de pertes Cp.
• Pour évaluer le couple de pertes Cp, on fait un essai à vide. Alors, Cu = 0 et le couple résistant est la somme :
- d'un couple de frottement sec Cfs, constant ; ce terme est en général négligé ;
- d'un couple de frottement visqueux proportionnel à la vitesse, avec un coefficient f appelé "constante de frottement visqueux".
Donc Cr = Cp = Cfs + f.  f.
On peut alors mettre la relation précédente sous la forme
dΩ
k.i - f.Ω = J. dt
(valable à vide seulement).
• Si, en plus, nous supposons en première approximation que l’inductance L de la machine reste faible par rapport à R, alors
u = E + R.i
et par conséquent,
u - E u - k.Ω
i = =
RR
. Finalement,
u - k.Ω dΩ
k. = J. + f.Ω
R dt
.
• Au démarrage, le couple d’inertie
J.dΩ / dt
étant beaucoup plus important que le couple de frottement visqueux, nous pouvons
négliger, en deuxième approximation, le terme
f.Ω
devant le terme
J.dΩ / dt
. Il vient alors la relation différentielle :
2
dΩ k u
J. + .Ω = k.
dt R R
, qui se met sous la forme canonique :
Cm
Cr0
-Cr0
0
- 0
0
r0
0
Ω
J. + C
t
0
r0
0
Ω
-J. - C
t
A
B
C
figure 5
E