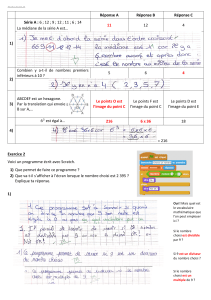
7 On dit que le carré d`un entier a même reste dans la division par 5

1L1-Option Mathématiques Devoir Maison 1
(Corrigé indicatif)
2006-1L option-DM01 O. WALTER http://www.chantematique.fr
7  On dit que le carré d'un entier a même reste dans la division par 5 que le carré du
chiffre de ses unités. Est-ce vrai ?
Réponse: un nombre n ayant pour chiffre des unités u s’écrit: n=10*k+u, où k est un
entier.
Son carré est n 2=(10k+u)2=100k 2+20ku+u 2=5() 20k 2+4ku +u 2.
Faire la division (euclidienne) d’un entier n par 5, c’est écrire n sous la forme
n=5q+r avec 0Âr<5.
Faisons donc la division (euclidienne) par 5 de u 2.
On a alors u 2=5q′+r avec 0Âr<5.
Mais alors n 2=5()
20k 2+4ku +5q′+r avec 0Âr<5, c’est-à-dire:
n 2=5() 20k 2+4ku+q′+r avec 0Âr<5.
Comme k, u et q’ sont des entiers, la somme Q=() 20k 2+4ku+q′ est également un entier.
On a donc montré:
n 2=5Q+r et u 2=5q′+r avec 0Âr<5.
Autrement dit: n 2 et u 2 ont le même reste dans la division (euclidienne) par 5.
8  Pourquoi le nombre qui s'écrit ababab est-il toujours divisible par 3 ?
Réponse: en base 10, ababab a pour somme de ses chiffres 3a+3b=3 (a+b). Or ce nombre
est manifestement un multiple de trois. D’après le critère de divisibilité par trois (démontré
en cours), ceci implique que ababab est aussi un multiple de trois (donc est divisible par 3).
9  Le carré d'un entier est soit un multiple de 3, soit un multiple de 3 augmenté de 1.
Prouvez-le !
Réponse: Un entier n est soit multiple de 3, soit égal à un multiple de 3 moins 1, soit à un
multiple de trois plus 1.En effet, un nombre entier sur trois est multiple de trois.
Donc n=3k ou n=3k-1, ou n=3k+1. Par suite son carré vaut n 2=9k 2=3*3k 2 ou n 2
=(3k−1)2=9k 2-6k+1=3() 3k 2-2k +1 ou
n 2=(3k+1)2=9k 2+6k+1=3() 3k 2+2k +1.
Dans le premier cas, n 2 est multiple de 3. Dans les deux autres cas, il est égal à un
multiple de 3 plus 1.
11  abcd est un nombre formé de quatre chiffres consécutifs dans l'ordre croissant. On
permute les deux chiffres de gauche pour obtenir bacd.
a) Le nombre obtenu est-il multiple de 11 ?
Réponse: Les chiffres sont consécutifs, donc b=a+1, c=a+2 et d=a+3. Le nombre obtenu
après permutation est, en base 10, égal à

1L1-Option Mathématiques Devoir Maison 1
(Corrigé indicatif)
2006-1L option-DM01 O. WALTER http://www.chantematique.fr
103b+102a+10c+d=103 (a+1)+102a+10(a+2)+a+3
=103a+103+102a+10a+20+a+3
=
()
103+102+10+1 a+103+20+3
= 1111a+1023
= 11*101*a+11*93
= 11 (101a+93).
Ceci montre que ce nombre est bien un multiple de 11.
b) Parmi tous ces nombres, un seul est un carré parfait. Lequel ?
Réponse: Le seul de ces nombres qui soit un carré est 4356=662 obtenu avec le chiffre
a=3.
Pour le vérifier, en mode table entrer y1=11(101X+93) et y2= X.
Régler alors la table pour compter de 0(start ou tblstart) à 10(end) avec un pas de 1( [ tbl ou
pitch) .
12  Un nombre de trois chiffres, écrit cdu, est divisible par 7. u est-il forcément divisible
par 7? et c+d+u? et c*d*u? et 2c + 3d + u ? et 5c–d+ 2u?
Réponse(s): on sait que cdu =100c+10d+u=7k puisqu’il est multiple de 7.
1) 700 est multiple de 7 évident et 0 son chiffre des unités ne l’est pas. Donc u n’est pas
forcément un multiple de 7.
2) 721=7*103 est multiple de 7 mais c+d+u=7+2+1=10 ne l’est pas.
3) 112=7*16 est multiple de 7 mais c*d*u=1*1*2=2 ne l’est pas.
4) cdu =100c+10d+u=(98+2)c+(7+3)d+u=98c+2c+7d+3d+u
=7*14c+7d+2c+3d+u
=7*(14c+d)+2c+3d+u.
Or, par hypothèse, cdu est multiple de 7. Comme 7*(14c+d) est un multiple de 7,
alors la différence cdu -7*(14c+d)=7*(k-14c-d) est un multiple de7.
Donc 2c+3d+u est un multiple de7.
5) Si cdu =112, alors 5c–d+ 2u=5*1-1+2*2=8. Et 8 n’est pas divisible par 7.