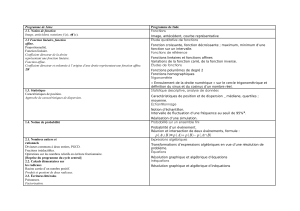
Aucun titre de diapositive - Cégep de Lévis

Montage préparé par :
André Ross
Professeur de mathématiques
Cégep de Lévis-Lauzon
Droites et plans,
positions relatives

Introduction
Des droites et des plans dans l’espace peuvent être parallèles,
concourants ou gauches. C’est ce qu’on appelle les positions
relatives des droites et des plans.
Nous verrons dans cette présentation les procédures pour
déterminer les positions relatives de droites dans R2ainsi que
de droites et de plans dans R3.

Positions relatives de droites dans R2
Droites parallèles
Caractéristiques des droites parallèles
Les vecteurs normaux sont parallèles :
Les vecteurs directeurs sont parallèles :
Le vecteur normal de l’une des droites
est perpendiculaire au vecteur directeur
de l’autre droite :
$kR tel que
$kR tel que
N1=k N2
D1=k D2
et N1•D2= 0D1•N2= 0

Positions relatives de droites dans R2
Droites parallèles
Caractéristiques des droites parallèles distinctes
•Lorsqu’un point R(x1;y1)est sur l’une des
droites, il ne peut être sur l’autre droite :
•Il n’y a aucun point d’intersection.
•Lorsqu’un point R(x1;y1)est sur l’une des
droites, il est sur l’autre droite :
•Il y a une infinité de points d’intersection.
Caractéristiques des droites parallèles confondues
si R ∆1, alors R ∆2
si R ∆1, alors R ∆2

Positions relatives de droites dans R2
Droites concourantes
Caractéristiques des droites concourantes
•Les droites ne sont pas parallèles.
•Les vecteurs directeurs sont non colinéaires :
•Le vecteur normal de l’une des droites
n’est pas perpendiculaire au vecteur
directeur de l’autre droite :
"kR\{0},
"kR\{0},
N1≠k N2
D1≠k D2
et D1•N2≠0N1•D2≠0
•Les vecteurs normaux sont non colinéaires :
•Il y a un seul point d’intersection.