Leçon Trigonométrie

Trigonométrie – Angles inscrits
I - Cosinus, sinus et tangente d’un angle aigu
Définitions : Dans un triangle rectangle :
• Le cosinus d’un angle aigu est le quotient de la longueur du côté adjacent à l’angle par la
longueur de l’hypoténuse.
• Le sinus d’un angle aigu est le quotient de la longueur du côté opposé à l’angle par la longueur de
l’hypoténuse.
• Le tangente d’un angle aigu est le quotient de la longueur du côté opposé à l’angle par la
longueur du côté adjacent à l’angle.
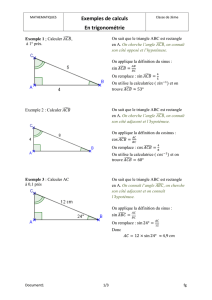
Exemple : Soit un triangle ABC rectangle en B.
côté adjacent à l'angle
cos hypoténuse
AB A
B AC AC
∧
∧
= =
côté opposé à l'angle
sin hypoténuse
BC A
B AC AC
∧
∧
= =
côté opposé à l'angle A
tan
côté adjacent à l'angle A
BC
B AC AB
∧
∧
∧
= =
Remarque : Le cosinus et le sinus d’un angle aigu sont des nombres compris entre 0 et 1.
Utilisation de la calculatrice
1)
sin40 0,64
≈
(Arrondi au centième) On tape : SIN 40 EXE
2)
7
tan
11
D E F
∧
=
32
D E F
∧
≈ °
(Arrondi au degré) On tape : SECONDE TAN ( 7
÷
11 ) EXE
II - Applications
1 - Calculer la mesure d’un angle aigu
Exemple 1 : Calculer la mesure de l’angle
J I K
∧
Dans le triangle IJK rectangle en J, on a :
sin
JK
J I K
IK
∧
=
3
sin
7,8
J I K
∧
=
On tape : SECONDE SIN (3
÷
7,8) EXE
23
J I K
∧
≈ °
(Arrondi au degré)
Côté adjacent à l’angle
A
∧
Côté opposé
à l’angle
A
∧
hypoténuse
On obtient tan
-
1
côté opposé
hypoténuse

Exemple 2 : Calculer la mesure de l’angle
S RT
∧
Dans le triangle RST rectangle en S, on a :
cos
RS
S RT
RT
∧
=
4,3
cos
6,3
S RT
∧
=
On tape : SECONDE COS (4,3
÷
6,3) EXE
47
S RT
∧
≈ °
(Arrondi au degré)
2 - Calculer une longueur
Exemple 1 : Calculer la longueur du segment [JK]
Dans le triangle JKL rectangle en J, on a :
tan
LJ
J K L
JK
∧
=
7,2
tan68
JK
=
D’après l’égalité du produit en croix,
tan68 7,2 1
JK
× = ×
7,2
tan68
JK =
2,9 cm
LK
≈
(Arrondi au dixième)
Exemple 2 : Calculer la longueur du segment [MN]
Dans le triangle MNP rectangle en M, on a :
sin
MN
N PM
NP
∧
=
sin45
6,2
MN
=
D’après l’égalité du produit en croix,
1 6,2 sin 45
MN
× = ×
4,4 cm
MN
≈
(Arrondi au dixième)
III - Propriétés
Dans un triangle rectangle, on considère x la mesure d’un angle aigu.
Propriété 1 :
( ) ( )
2 2
cos sin 1
x x
+ =
Démonstration : Soit ABC un triangle rectangle en B.
D’après le théorème de Pythagore, on a :
2 2 2
AB BC AC
+ =
2 2 2
2 2
AB BC AC
AC AC
+=
(Règle sur les équations)
côté adjacent
hypoténuse
côté opposé
hypoténuse
côté opposé
longueur cherchée
côté adjacent
longueur cherchée

2 2
2 2
1
AB BC
AC AC
+ =
(Règle sur les fractions)
2 2
1
AB BC
AC AC
+ =
    (Règle sur les puissances)
( ) ( )
2 2
cos sin 1
x x
+ =
Propriété 2 :
sin
tan
cos
x
x
x
=
Démonstration : Soit ABC un triangle rectangle en B.
sin
cos
BC
x
AC
AB
x
AC
=
sin
cos
x BC AC
x AC AB
= ×
sin
cos
x BC AC
x AC AB
×
=× (Règle sur les fractions)
sin
cos
x BC
x AB
=
sin
tan
cos
x
x
x
=
IV - Angle inscrit et angle au centre
1 - Angle inscrit
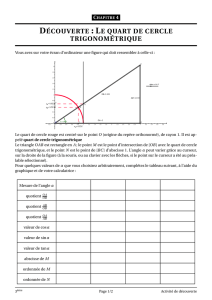
Définition : Dans un cercle, un angle inscrit est un angle dont le sommet est un point du cercle et
dont les côtés coupent ce cercle.
Théorème 1 : Si dans un cercle, deux angles inscrits interceptent le même arc alors ils sont de
même mesure.
Données
Dans le cercle C
CC
C,
C AD
∧
et
C B D
∧
sont des
angles inscrits.
C AD
∧
et
C B D
∧
interceptent le même arc CD
Conclusion
C AD C B D
∧ ∧
=
C
CC
C
C
CC
C

2 - Angle au centre
Définition : Dans un cercle, un angle au centre est un angle dont le sommet est le centre du cercle
et dont les côtés coupent ce cercle.
Théorème 2 : Si dans un cercle, un angle au centre et un angle inscrit interceptent le même arc alors
l’angle au centre mesure le double de l’angle inscrit.
Données
Dans le cercle C
CC
C,
BOC
∧
est un angle au centre et
B AC
∧
est un angle inscrit.
BOC
∧
et
B AC
∧
interceptent le même arc BC.
Conclusion
2
BOC B AC
∧ ∧
= ×
3 - Application
Soit RST un triangle équilatéral inscrit dans un cercle C
CC
C de centre O.
Quelle est la mesure de l’angle
ROS
∧
? Justifier.
• RST est un triangle équilatéral.
•• Or, si un triangle est équilatéral alors ses trois angles mesurent 60°.
••• Donc
60
RT S
∧
= °
.
• Dans le cercle C
CC
C,
ROS
∧
est un angle au centre et
RT S
∧
est un angle inscrit.
ROS
∧
et
RT S
∧
interceptent le même arc RS.
•• Or, si dans un cercle un angle au centre et un angle inscrit interceptent le même arc alors l’angle
au centre mesure le double de l’angle inscrit.
••• Donc 2
ROS RT S
∧ ∧
= ×
2 60
ROS
∧
= ×
120
ROS
∧
= °
C
CC
C
C
CC
C